Michael Madden
Graph Convolutional Networks: analysis, improvements and results
Dec 19, 2019


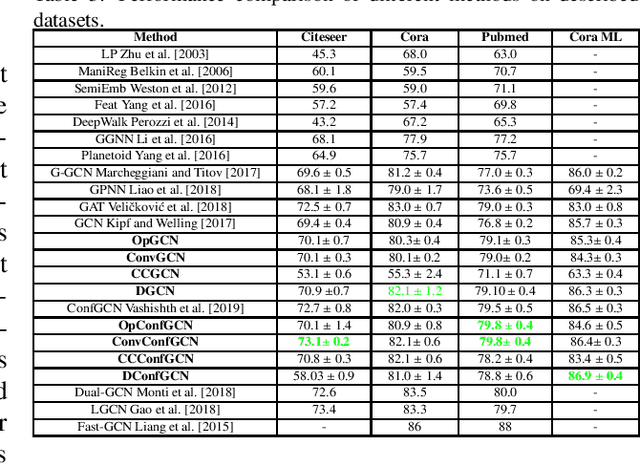
Abstract:In the current era of neural networks and big data, higher dimensional data is processed for automation of different application areas. Graphs represent a complex data organization in which dependencies between more than one object or activity occur. Due to the high dimensionality, this data creates challenges for machine learning algorithms. Graph convolutional networks were introduced to utilize the convolutional models concepts that shows good results. In this context, we enhanced two of the existing Graph convolutional network models by proposing four enhancements. These changes includes: hyper parameters optimization, convex combination of activation functions, topological information enrichment through clustering coefficients measure, and structural redesign of the network through addition of dense layers. We present extensive results on four state-of-art benchmark datasets. The performance is notable not only in terms of lesser computational cost compared to competitors, but also achieved competitive results for three of the datasets and state-of-the-art for the fourth dataset.
Dealing with Stochasticity in Biological ODE Models
Oct 14, 2019

Abstract:Mathematical modeling with Ordinary Differential Equations (ODEs) has proven to be extremely successful in a variety of fields, including biology. However, these models are completely deterministic given a certain set of initial conditions. We convert mathematical ODE models of three benchmark biological systems to Dynamic Bayesian Networks (DBNs). The DBN model can handle model uncertainty and data uncertainty in a principled manner. They can be used for temporal data mining for noisy and missing variables. We apply Particle Filtering algorithm to infer the model variables by re-estimating the models parameters of various biological ODE models. The model parameters are automatically re-estimated using temporal evidence in the form of data streams. The results show that DBNs are capable of inferring the model variables of the ODE model with high accuracy in situations where data is missing, incomplete, sparse and irregular and true values of model parameters are not known.
PROFET: Construction and Inference of DBNs Based on Mathematical Models
Oct 14, 2019



Abstract:This paper presents, evaluates, and discusses a new software tool to automatically build Dynamic Bayesian Networks (DBNs) from ordinary differential equations (ODEs) entered by the user. The DBNs generated from ODE models can handle both data uncertainty and model uncertainty in a principled manner. The application, named PROFET, can be used for temporal data mining with noisy or missing variables. It enables automatic re-estimation of model parameters using temporal evidence in the form of data streams. For temporal inference, PROFET includes both standard fixed time step particle filtering and its extension, adaptive-time particle filtering algorithms. Adaptive-time particle filtering enables the DBN to automatically adapt its time step length to match the dynamics of the model. We demonstrate PROFET's functionality by using it to infer the model variables by estimating the model parameters of four benchmark ODE systems. From the generation of the DBN model to temporal inference, the entire process is automated and is delivered as an open-source platform-independent software application with a comprehensive user interface. PROFET is released under the Apache License 2.0. Its source code, executable and documentation are available at http:://profet.it.nuigalway.ie.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge