Quantum Annealing for Computer Vision Minimization Problems

Computer Vision (CV) labelling algorithms play a pivotal role in the domain of low-level vision. For decades, it has been known that these problems can be elegantly formulated as discrete energy minimization problems derived from probabilistic graphical models (such as Markov Random Fields). Despite recent advances in inference algorithms (such as graph-cut and message-passing algorithms), the resulting energy minimization problems are generally viewed as intractable. The emergence of quantum computations, which offer the potential for faster solutions to certain problems than classical methods, has led to an increased interest in utilizing quantum properties to overcome intractable problems. Recently, there has also been a growing interest in Quantum Computer Vision (QCV), with the hope of providing a credible alternative or assistant to deep learning solutions in the field. This study investigates a new Quantum Annealing based inference algorithm for CV discrete energy minimization problems. Our contribution is focused on Stereo Matching as a significant CV labeling problem. As a proof of concept, we also use a hybrid quantum-classical solver provided by D-Wave System to compare our results with the best classical inference algorithms in the literature.

Nondeterminism and Instability in Neural Network Optimization

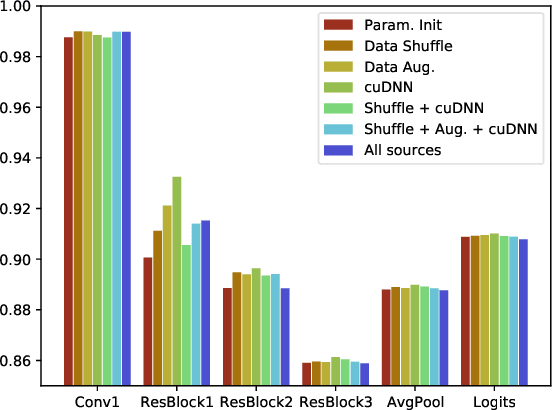
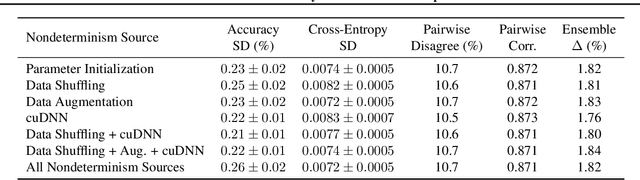
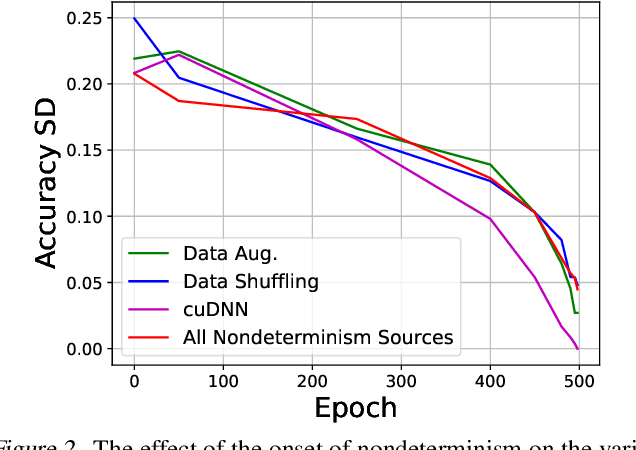
Nondeterminism in neural network optimization produces uncertainty in performance, making small improvements difficult to discern from run-to-run variability. While uncertainty can be reduced by training multiple model copies, doing so is time-consuming, costly, and harms reproducibility. In this work, we establish an experimental protocol for understanding the effect of optimization nondeterminism on model diversity, allowing us to isolate the effects of a variety of sources of nondeterminism. Surprisingly, we find that all sources of nondeterminism have similar effects on measures of model diversity. To explain this intriguing fact, we identify the instability of model training, taken as an end-to-end procedure, as the key determinant. We show that even one-bit changes in initial parameters result in models converging to vastly different values. Last, we propose two approaches for reducing the effects of instability on run-to-run variability.

Improved Adversarial Robustness via Logit Regularization Methods

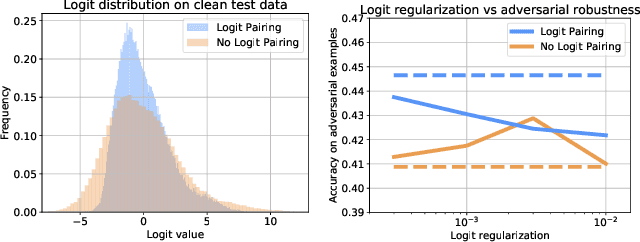
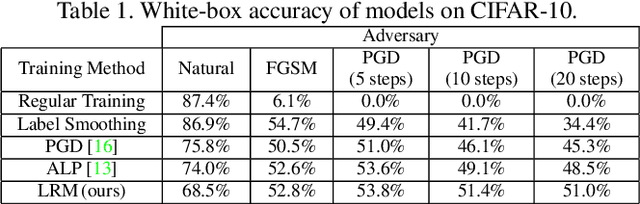
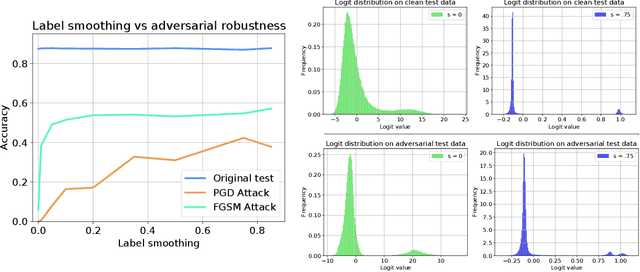
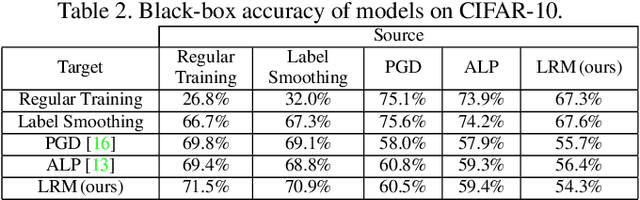
While great progress has been made at making neural networks effective across a wide range of visual tasks, most models are surprisingly vulnerable. This frailness takes the form of small, carefully chosen perturbations of their input, known as adversarial examples, which represent a security threat for learned vision models in the wild -- a threat which should be responsibly defended against in safety-critical applications of computer vision. In this paper, we advocate for and experimentally investigate the use of a family of logit regularization techniques as an adversarial defense, which can be used in conjunction with other methods for creating adversarial robustness at little to no marginal cost. We also demonstrate that much of the effectiveness of one recent adversarial defense mechanism can in fact be attributed to logit regularization, and show how to improve its defense against both white-box and black-box attacks, in the process creating a stronger black-box attack against PGD-based models. We validate our methods on three datasets and include results on both gradient-free attacks and strong gradient-based iterative attacks with as many as 1,000 steps.

Four Things Everyone Should Know to Improve Batch Normalization

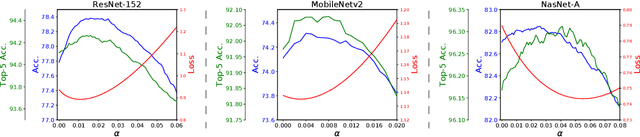
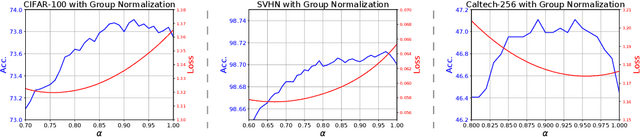
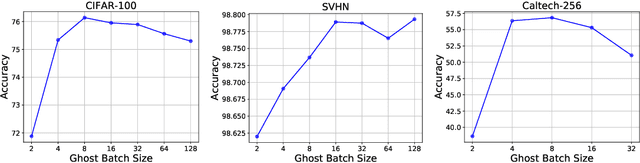
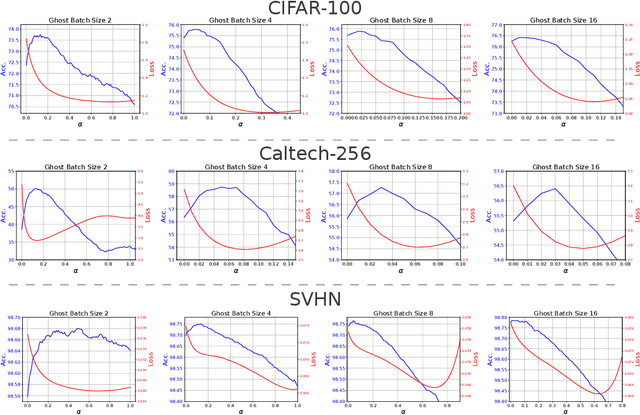
A key component of most neural network architectures is the use of normalization layers, such as Batch Normalization. Despite its common use and large utility in optimizing deep architectures that are otherwise intractable, it has been challenging both to generically improve upon Batch Normalization and to understand specific circumstances that lend themselves to other enhancements. In this paper, we identify four improvements to the generic form of Batch Normalization and the circumstances under which they work, yielding performance gains across all batch sizes while requiring no additional computation during training. These contributions include proposing a method for reasoning about the current example in inference normalization statistics which fixes a training vs. inference discrepancy; recognizing and validating the powerful regularization effect of Ghost Batch Normalization for small and medium batch sizes; examining the effect of weight decay regularization on the scaling and shifting parameters; and identifying a new normalization algorithm for very small batch sizes by combining the strengths of Batch and Group Normalization. We validate our results empirically on four datasets: CIFAR-100, SVHN, Caltech-256, and ImageNet.

Improved Mixed-Example Data Augmentation

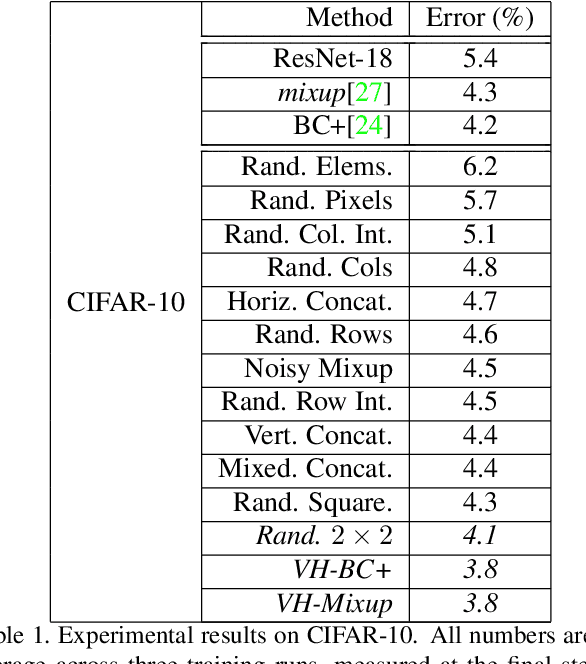
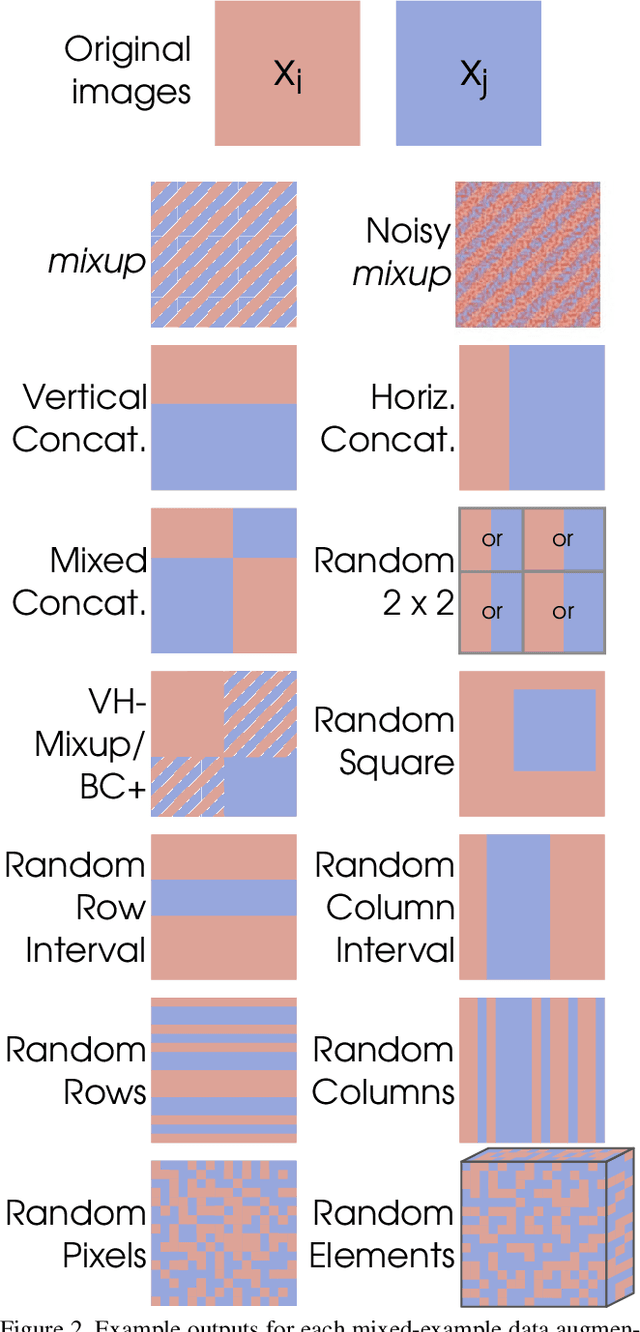
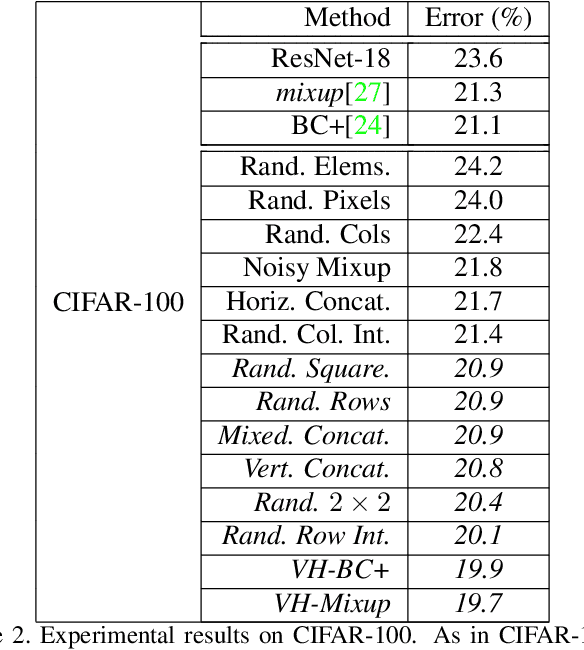
In order to reduce overfitting, neural networks are typically trained with data augmentation, the practice of artificially generating additional training data via label-preserving transformations of existing training examples. While these types of transformations make intuitive sense, recent work has demonstrated that even non-label-preserving data augmentation can be surprisingly effective, examining this type of data augmentation through linear combinations of pairs of examples. Despite their effectiveness, little is known about why such methods work. In this work, we aim to explore a new, more generalized form of this type of data augmentation in order to determine whether such linearity is necessary. By considering this broader scope of "mixed-example data augmentation", we find a much larger space of practical augmentation techniques, including methods that improve upon previous state-of-the-art. This generalization has benefits beyond the promise of improved performance, revealing a number of types of mixed-example data augmentation that are radically different from those considered in prior work, which provides evidence that current theories for the effectiveness of such methods are incomplete and suggests that any such theory must explain a much broader phenomenon.

New Solutions to the Firing Squad Synchronization Problems for Neural and Hyperdag P Systems

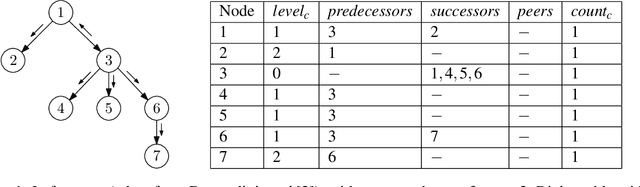
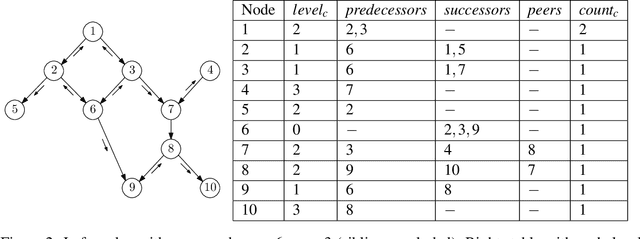
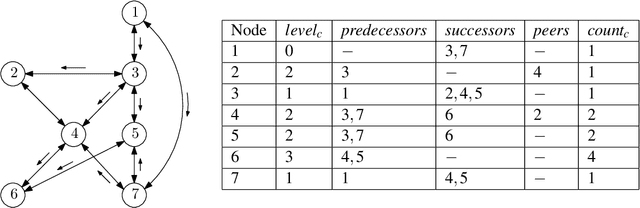
We propose two uniform solutions to an open question: the Firing Squad Synchronization Problem (FSSP), for hyperdag and symmetric neural P systems, with anonymous cells. Our solutions take e_c+5 and 6e_c+7 steps, respectively, where e_c is the eccentricity of the commander cell of the dag or digraph underlying these P systems. The first and fast solution is based on a novel proposal, which dynamically extends P systems with mobile channels. The second solution is substantially longer, but is solely based on classical rules and static channels. In contrast to the previous solutions, which work for tree-based P systems, our solutions synchronize to any subset of the underlying digraph; and do not require membrane polarizations or conditional rules, but require states, as typically used in hyperdag and neural P systems.