Improved Mixed-Example Data Augmentation

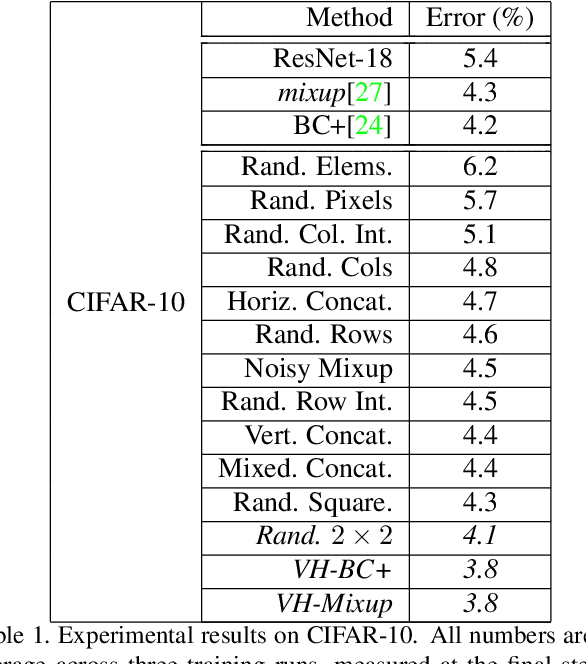
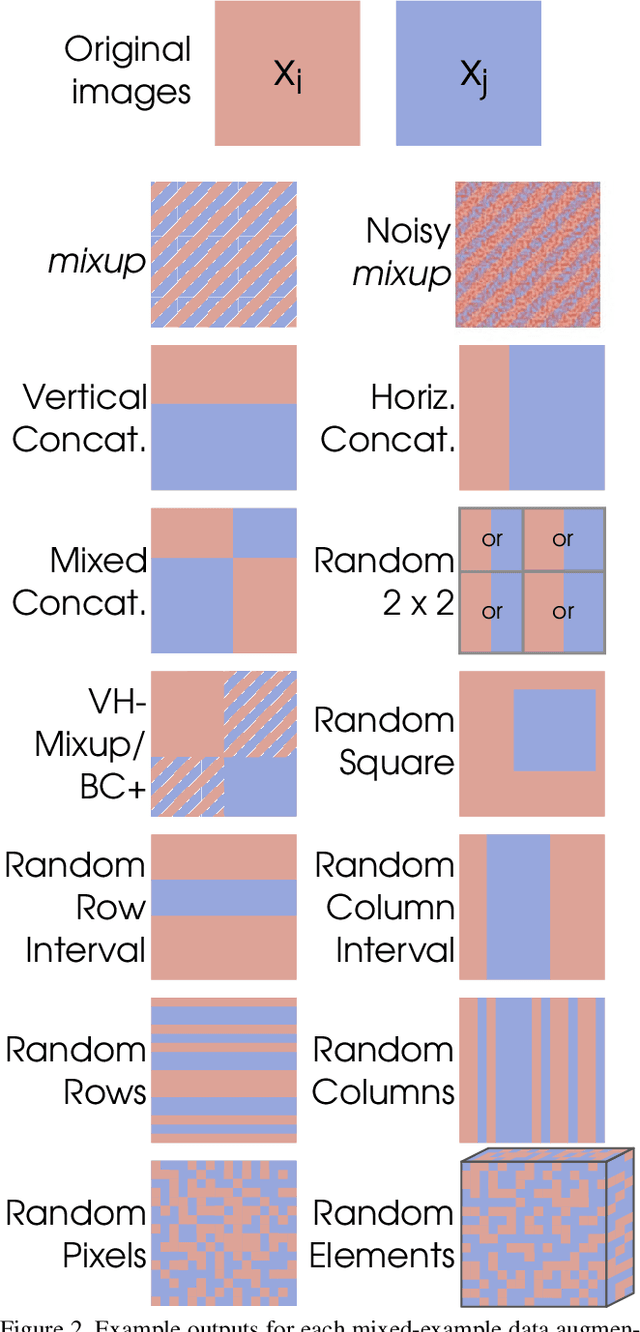
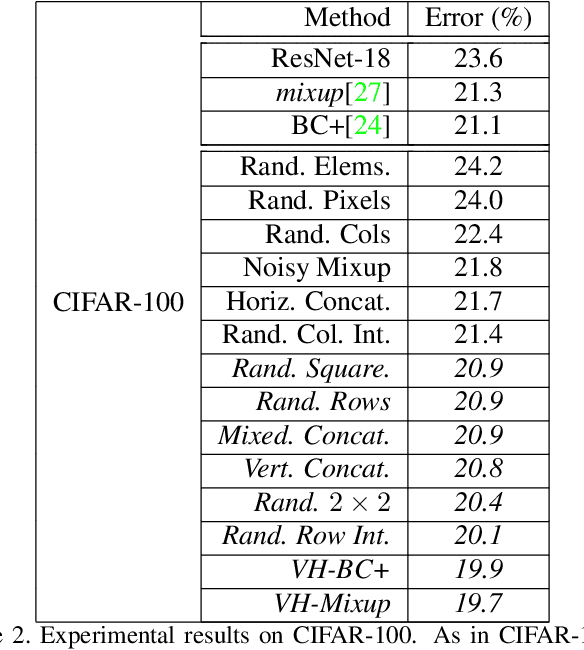
In order to reduce overfitting, neural networks are typically trained with data augmentation, the practice of artificially generating additional training data via label-preserving transformations of existing training examples. While these types of transformations make intuitive sense, recent work has demonstrated that even non-label-preserving data augmentation can be surprisingly effective, examining this type of data augmentation through linear combinations of pairs of examples. Despite their effectiveness, little is known about why such methods work. In this work, we aim to explore a new, more generalized form of this type of data augmentation in order to determine whether such linearity is necessary. By considering this broader scope of "mixed-example data augmentation", we find a much larger space of practical augmentation techniques, including methods that improve upon previous state-of-the-art. This generalization has benefits beyond the promise of improved performance, revealing a number of types of mixed-example data augmentation that are radically different from those considered in prior work, which provides evidence that current theories for the effectiveness of such methods are incomplete and suggests that any such theory must explain a much broader phenomenon.