Using the SEKF to Transfer NN Models of Dynamical Systems with Limited Data

Data-driven models of dynamical systems require extensive amounts of training data. For many practical applications, gathering sufficient data is not feasible due to cost or safety concerns. This work uses the Subset Extended Kalman Filter (SEKF) to adapt pre-trained neural network models to new, similar systems with limited data available. Experimental validation across damped spring and continuous stirred-tank reactor systems demonstrates that small parameter perturbations to the initial model capture target system dynamics while requiring as little as 1% of original training data. In addition, finetuning requires less computational cost and reduces generalization error.

Short-Term Solar Irradiance Forecasting Under Data Transmission Constraints

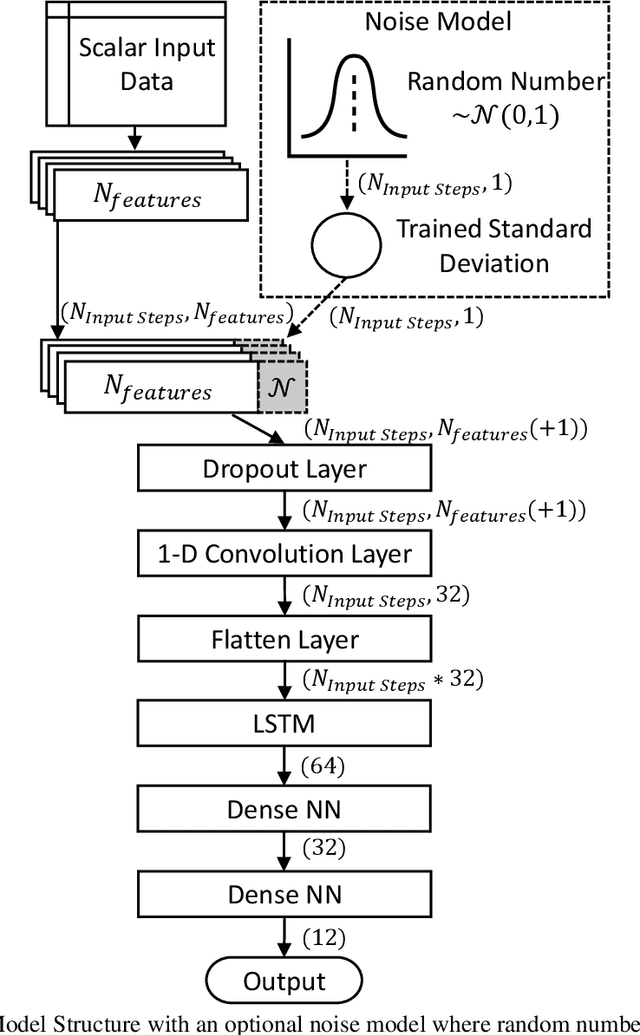
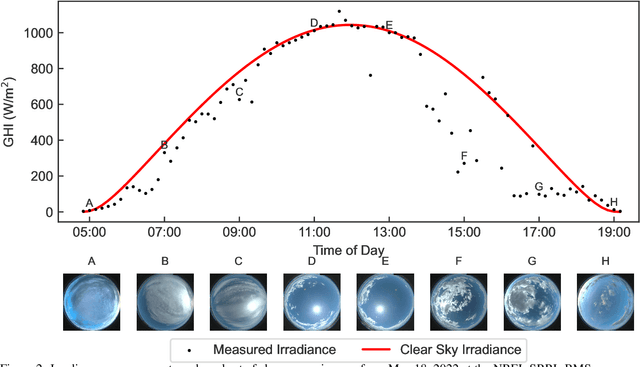
We report a data-parsimonious machine learning model for short-term forecasting of solar irradiance. The model inputs include sky camera images that are reduced to scalar features to meet data transmission constraints. The output irradiance values are transformed to focus on unknown short-term dynamics. Inspired by control theory, a noise input is used to reflect unmeasured variables and is shown to improve model predictions, often considerably. Five years of data from the NREL Solar Radiation Research Laboratory were used to create three rolling train-validate sets and determine the best representations for time, the optimal span of input measurements, and the most impactful model input data (features). For the chosen test data, the model achieves a mean absolute error of 74.34 $W/m^2$ compared to a baseline 134.35 $W/m^2$ using the persistence of cloudiness model.

DySMHO: Data-Driven Discovery of Governing Equations for Dynamical Systems via Moving Horizon Optimization

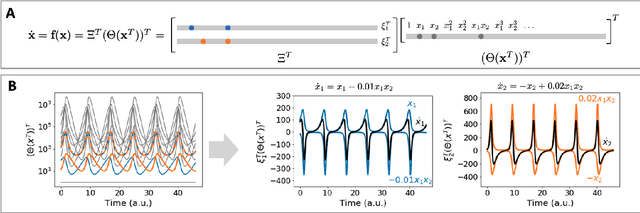
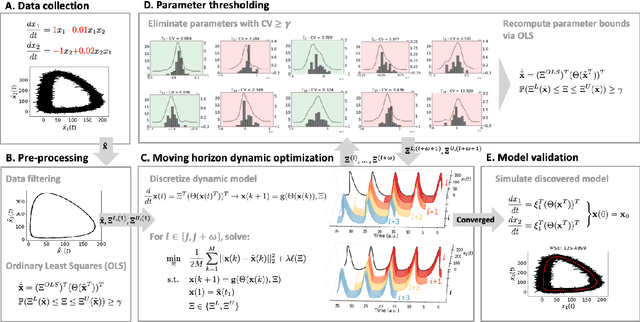
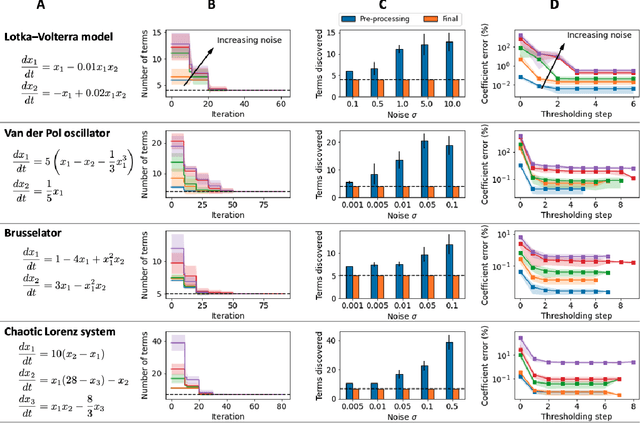
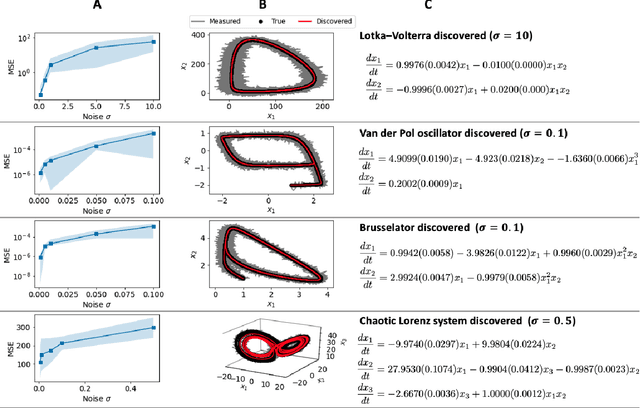
Discovering the governing laws underpinning physical and chemical phenomena is a key step towards understanding and ultimately controlling systems in science and engineering. We introduce Discovery of Dynamical Systems via Moving Horizon Optimization (DySMHO), a scalable machine learning framework for identifying governing laws in the form of differential equations from large-scale noisy experimental data sets. DySMHO consists of a novel moving horizon dynamic optimization strategy that sequentially learns the underlying governing equations from a large dictionary of basis functions. The sequential nature of DySMHO allows leveraging statistical arguments for eliminating irrelevant basis functions, avoiding overfitting to recover accurate and parsimonious forms of the governing equations. Canonical nonlinear dynamical system examples are used to demonstrate that DySMHO can accurately recover the governing laws, is robust to high levels of measurement noise and that it can handle challenges such as multiple time scale dynamics.