DySMHO: Data-Driven Discovery of Governing Equations for Dynamical Systems via Moving Horizon Optimization
Paper and Code
Jul 30, 2021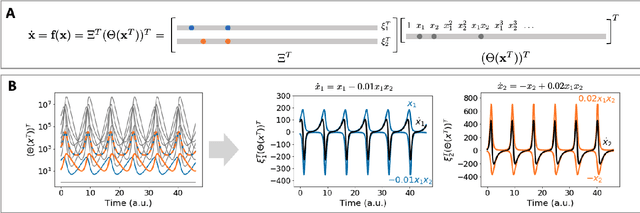
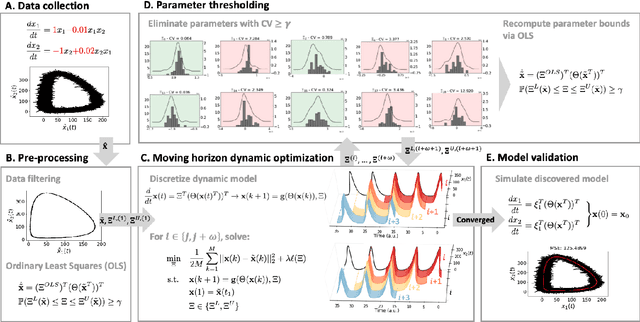
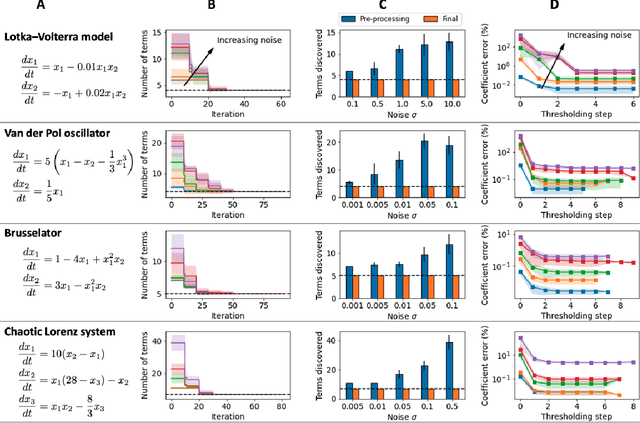
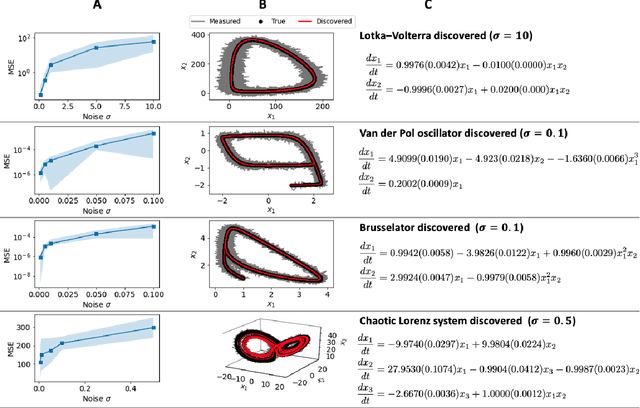
Discovering the governing laws underpinning physical and chemical phenomena is a key step towards understanding and ultimately controlling systems in science and engineering. We introduce Discovery of Dynamical Systems via Moving Horizon Optimization (DySMHO), a scalable machine learning framework for identifying governing laws in the form of differential equations from large-scale noisy experimental data sets. DySMHO consists of a novel moving horizon dynamic optimization strategy that sequentially learns the underlying governing equations from a large dictionary of basis functions. The sequential nature of DySMHO allows leveraging statistical arguments for eliminating irrelevant basis functions, avoiding overfitting to recover accurate and parsimonious forms of the governing equations. Canonical nonlinear dynamical system examples are used to demonstrate that DySMHO can accurately recover the governing laws, is robust to high levels of measurement noise and that it can handle challenges such as multiple time scale dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge