Generating Object Cluster Hierarchies for Benchmarking

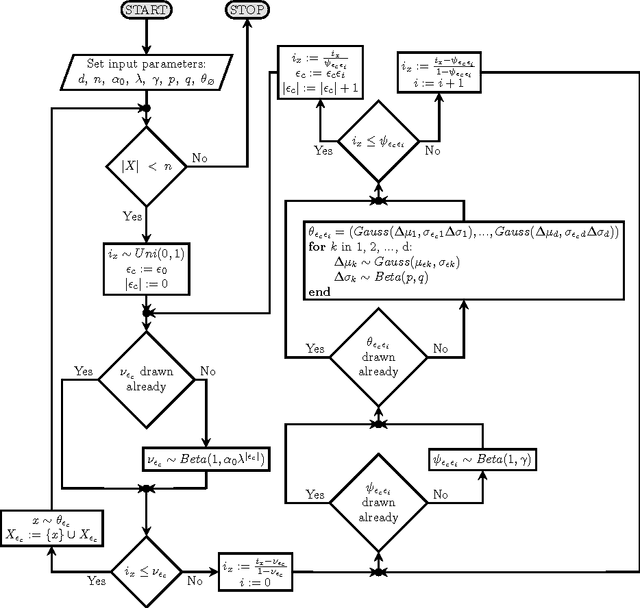
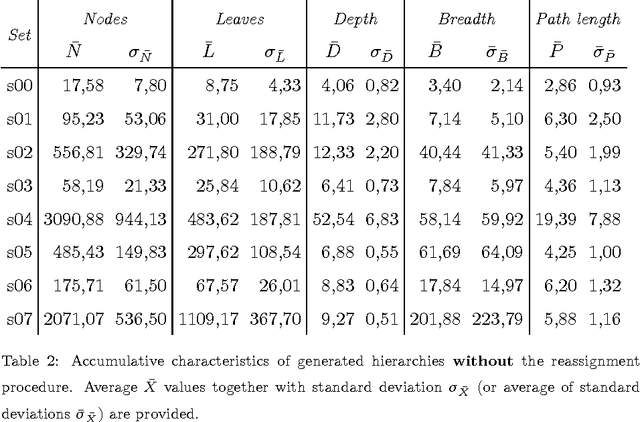
The field of Machine Learning and the topic of clustering within it is still widely researched. Recently, researchers became interested in a new variant of hierarchical clustering, where hierarchical (partial order) relationships exist not only between clusters but also objects. In this variant of clustering, objects can be assigned not only to leave, but other properties are also defined. Although examples of this approach already exist in literature, the authors have encountered a problem with the analysis and comparison of obtained results. The problem is twofold. Firstly, there is a lack of evaluation methods. Secondly, there is a lack of available benchmark data, at least the authors failed to find them. The aim of this work is to fill the second gap. The main contribution of this paper is a new method of generating hierarchical structures of data. Additionally, the paper includes a theoretical analysis of the generation parameters and their influence on the results. Comprehensive experiments are presented and discussed. The dataset generator and visualiser tools developed are publicly available for use (http://kio.pwr.edu.pl/?page_id=396).

Hierarchy of Groups Evaluation Using Different F-score Variants

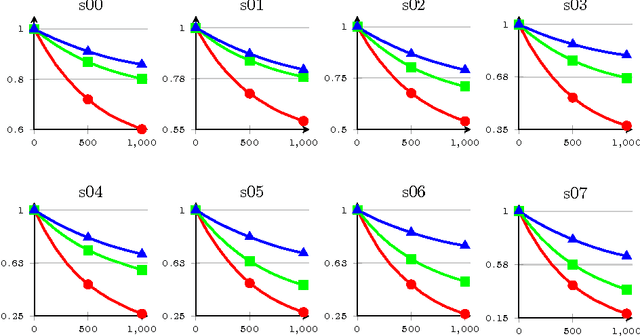
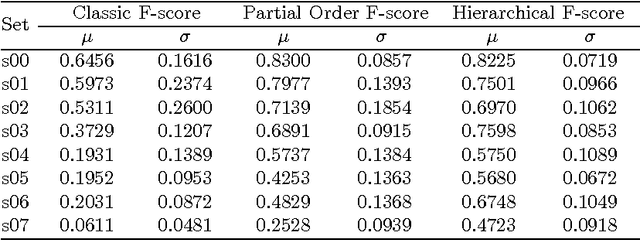
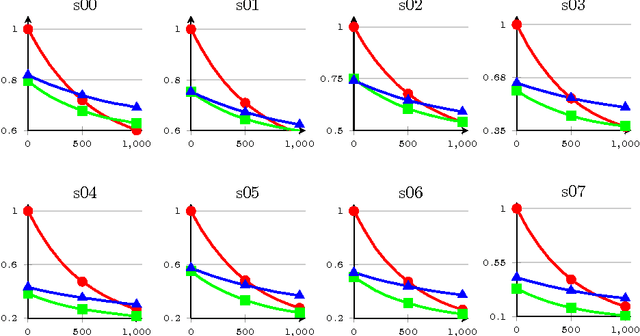
The paper presents a cursory examination of clustering, focusing on a rarely explored field of hierarchy of clusters. Based on this, a short discussion of clustering quality measures is presented and the F-score measure is examined more deeply. As there are no attempts to assess the quality for hierarchies of clusters, three variants of the F-Score based index are presented: classic, hierarchical and partial order. The partial order index is the authors' approach to the subject. Conducted experiments show the properties of the considered measures. In conclusions, the strong and weak sides of each variant are presented.