A hybrid estimation of distribution algorithm for joint stratification and sample allocation

In this study we propose a hybrid estimation of distribution algorithm (HEDA) to solve the joint stratification and sample allocation problem. This is a complex problem in which each the quality of each stratification from the set of all possible stratifications is measured its optimal sample allocation. EDAs are stochastic black-box optimization algorithms which can be used to estimate, build and sample probability models in the search for an optimal stratification. In this paper we enhance the exploitation properties of the EDA by adding a simulated annealing algorithm to make it a hybrid EDA. Results of empirical comparisons for atomic and continuous strata show that the HEDA attains the bests results found so far when compared to benchmark tests on the same data using a grouping genetic algorithm, simulated annealing algorithm or hill-climbing algorithm. However, the execution times and total execution are, in general, higher for the HEDA.

Combining K-means type algorithms with Hill Climbing for Joint Stratification and Sample Allocation Designs

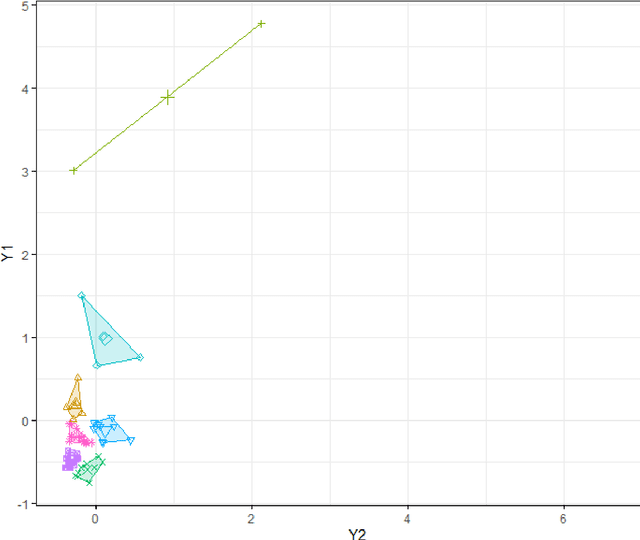
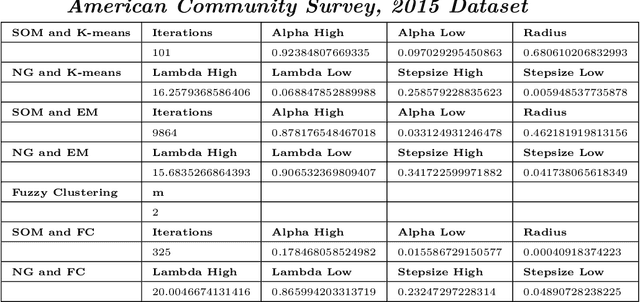
In this paper we combine the k-means and/or k-means type algorithms with a hill climbing algorithm in stages to solve the joint stratification and sample allocation problem. This is a combinatorial optimisation problem in which we search for the optimal stratification from the set of all possible stratifications of basic strata. Each stratification being a solution the quality of which is measured by its cost. This problem is intractable for larger sets. Furthermore evaluating the cost of each solution is expensive. A number of heuristic algorithms have already been developed to solve this problem with the aim of finding acceptable solutions in reasonable computation times. However, the heuristics for these algorithms need to be trained in order to optimise performance in each instance. We compare the above multi-stage combination of algorithms with three recent algorithms and report the solution costs, evaluation times and training times. The multi-stage combinations generally compare well with the recent algorithms both in the case of atomic and continuous strata and provide the survey designer with a greater choice of algorithms to choose from.

A Simulated Annealing Algorithm for Joint Stratification and Sample Allocation Designs

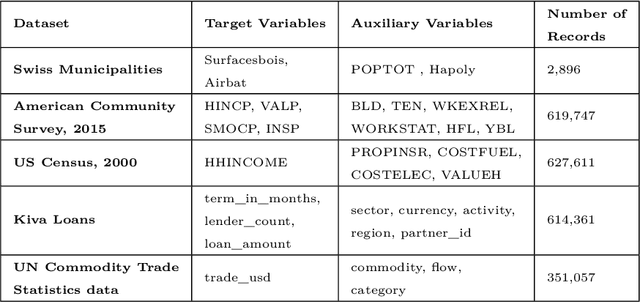
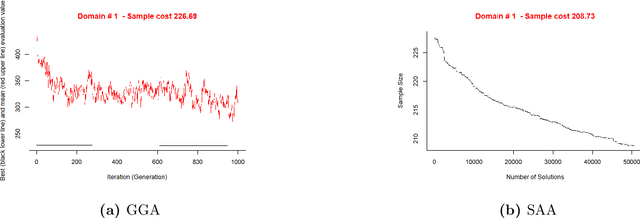
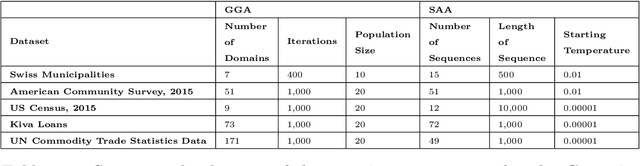
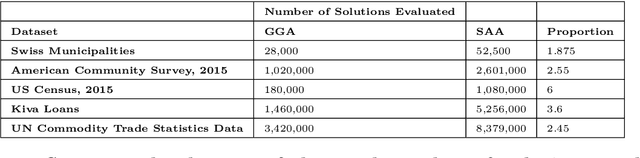
This study combined simulated annealing with delta evaluation to solve the joint stratification and sample allocation problem. In this problem, atomic strata are partitioned into mutually exclusive and collectively exhaustive strata. Each stratification is a solution, the quality of which is measured by its cost. The Bell number of possible solutions is enormous for even a moderate number of atomic strata and an additional layer of complexity is added with the evaluation time of each solution. Many larger scale combinatorial optimisation problems cannot be solved to optimality because the search for an optimum solution requires a prohibitive amount of computation time; a number of local search heuristic algorithms have been designed for this problem but these can become trapped in local minima preventing any further improvements. We add to the existing suite of local search algorithms with a simulated annealing algorithm that allows for an escape from local minima and uses delta evaluation to exploit the similarity between consecutive solutions and thereby reduce the evaluation time.