Mehrdad Maleki
Recent Trends in Modelling the Continuous Time Series using Deep Learning: A Survey
Sep 13, 2024



Abstract:Continuous-time series is essential for different modern application areas, e.g. healthcare, automobile, energy, finance, Internet of things (IoT) and other related areas. Different application needs to process as well as analyse a massive amount of data in time series structure in order to determine the data-driven result, for example, financial trend prediction, potential probability of the occurrence of a particular event occurrence identification, patient health record processing and so many more. However, modeling real-time data using a continuous-time series is challenging since the dynamical systems behind the data could be a differential equation. Several research works have tried to solve the challenges of modelling the continuous-time series using different neural network models and approaches for data processing and learning. The existing deep learning models are not free from challenges and limitations due to diversity among different attributes, behaviour, duration of steps, energy, and data sampling rate. This paper has described the general problem domain of time series and reviewed the challenges of modelling the continuous time series. We have presented a comparative analysis of recent developments in deep learning models and their contribution to solving different difficulties of modelling the continuous time series. We have also identified the limitations of the existing neural network model and open issues. The main goal of this review is to understand the recent trend of neural network models used in a different real-world application with continuous-time data.
HeunNet: Extending ResNet using Heun's Methods
May 14, 2021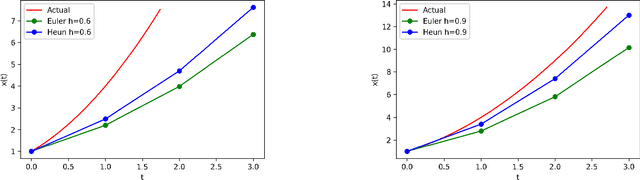
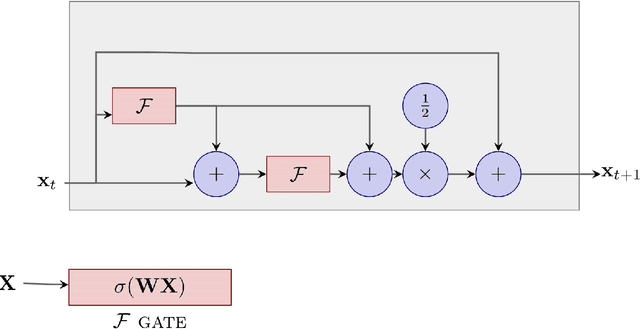
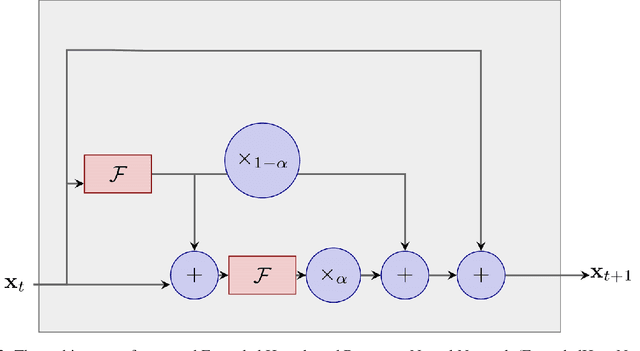
Abstract:There is an analogy between the ResNet (Residual Network) architecture for deep neural networks and an Euler solver for an ODE. The transformation performed by each layer resembles an Euler step in solving an ODE. We consider the Heun Method, which involves a single predictor-corrector cycle, and complete the analogy, building a predictor-corrector variant of ResNet, which we call a HeunNet. Just as Heun's method is more accurate than Euler's, experiments show that HeunNet achieves high accuracy with low computational (both training and test) time compared to both vanilla recurrent neural networks and other ResNet variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge