Mehmet Gönen
BaTFLED: Bayesian Tensor Factorization Linked to External Data
Dec 22, 2016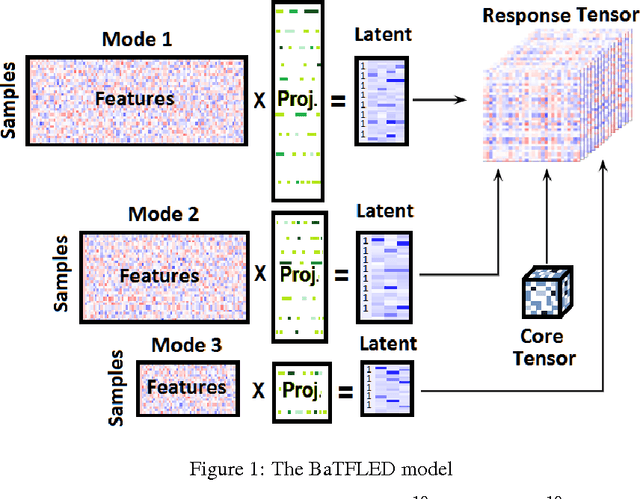
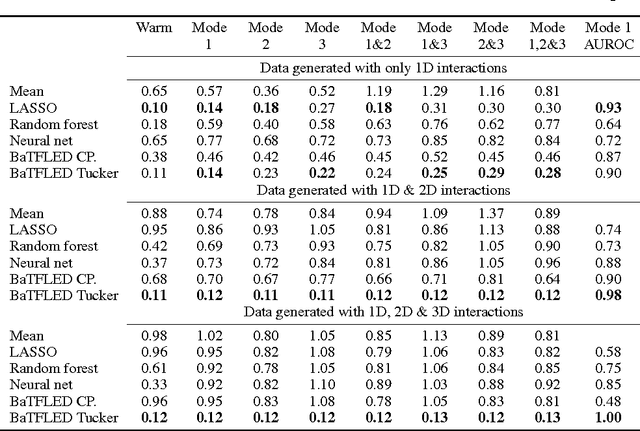
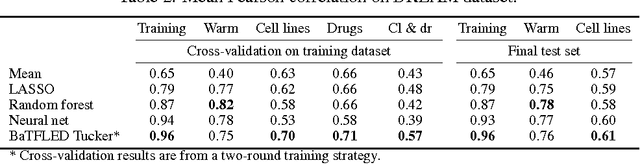
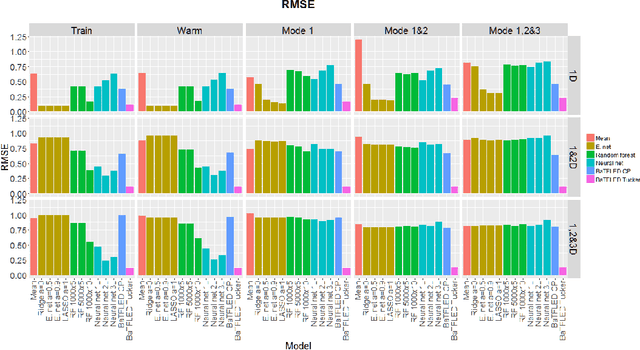
Abstract:The vast majority of current machine learning algorithms are designed to predict single responses or a vector of responses, yet many types of response are more naturally organized as matrices or higher-order tensor objects where characteristics are shared across modes. We present a new machine learning algorithm BaTFLED (Bayesian Tensor Factorization Linked to External Data) that predicts values in a three-dimensional response tensor using input features for each of the dimensions. BaTFLED uses a probabilistic Bayesian framework to learn projection matrices mapping input features for each mode into latent representations that multiply to form the response tensor. By utilizing a Tucker decomposition, the model can capture weights for interactions between latent factors for each mode in a small core tensor. Priors that encourage sparsity in the projection matrices and core tensor allow for feature selection and model regularization. This method is shown to far outperform elastic net and neural net models on 'cold start' tasks from data simulated in a three-mode structure. Additionally, we apply the model to predict dose-response curves in a panel of breast cancer cell lines treated with drug compounds that was used as a Dialogue for Reverse Engineering Assessments and Methods (DREAM) challenge.
Kernelized Bayesian Matrix Factorization
May 08, 2013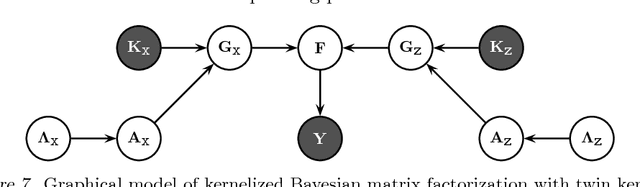
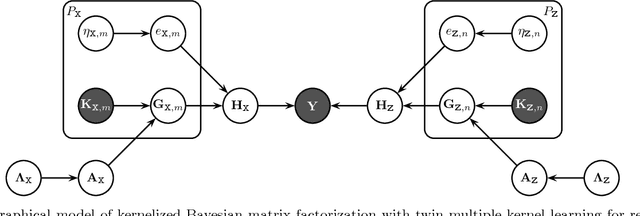
Abstract:We extend kernelized matrix factorization with a fully Bayesian treatment and with an ability to work with multiple side information sources expressed as different kernels. Kernel functions have been introduced to matrix factorization to integrate side information about the rows and columns (e.g., objects and users in recommender systems), which is necessary for making out-of-matrix (i.e., cold start) predictions. We discuss specifically bipartite graph inference, where the output matrix is binary, but extensions to more general matrices are straightforward. We extend the state of the art in two key aspects: (i) A fully conjugate probabilistic formulation of the kernelized matrix factorization problem enables an efficient variational approximation, whereas fully Bayesian treatments are not computationally feasible in the earlier approaches. (ii) Multiple side information sources are included, treated as different kernels in multiple kernel learning that additionally reveals which side information sources are informative. Our method outperforms alternatives in predicting drug-protein interactions on two data sets. We then show that our framework can also be used for solving multilabel learning problems by considering samples and labels as the two domains where matrix factorization operates on. Our algorithm obtains the lowest Hamming loss values on 10 out of 14 multilabel classification data sets compared to five state-of-the-art multilabel learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge