Solving Linear Equations Using a Jacobi Based Time-Variant Adaptive Hybrid Evolutionary Algorithm

Large set of linear equations, especially for sparse and structured coefficient (matrix) equations, solutions using classical methods become arduous. And evolutionary algorithms have mostly been used to solve various optimization and learning problems. Recently, hybridization of classical methods (Jacobi method and Gauss-Seidel method) with evolutionary computation techniques have successfully been applied in linear equation solving. In the both above hybrid evolutionary methods, uniform adaptation (UA) techniques are used to adapt relaxation factor. In this paper, a new Jacobi Based Time-Variant Adaptive (JBTVA) hybrid evolutionary algorithm is proposed. In this algorithm, a Time-Variant Adaptive (TVA) technique of relaxation factor is introduced aiming at both improving the fine local tuning and reducing the disadvantage of uniform adaptation of relaxation factors. This algorithm integrates the Jacobi based SR method with time variant adaptive evolutionary algorithm. The convergence theorems of the proposed algorithm are proved theoretically. And the performance of the proposed algorithm is compared with JBUA hybrid evolutionary algorithm and classical methods in the experimental domain. The proposed algorithm outperforms both the JBUA hybrid algorithm and classical methods in terms of convergence speed and effectiveness.

An Approach to Solve Linear Equations Using a Time-Variant Adaptation Based Hybrid Evolutionary Algorithm

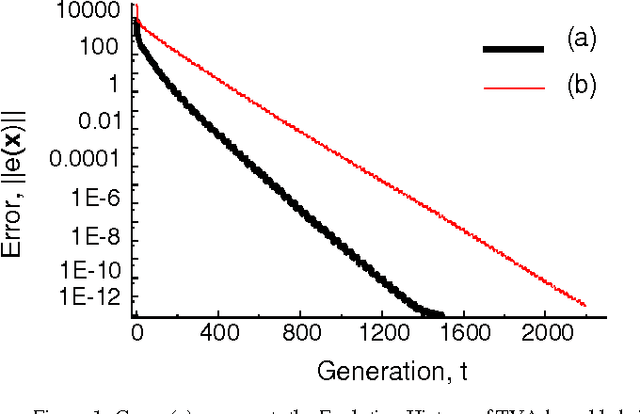
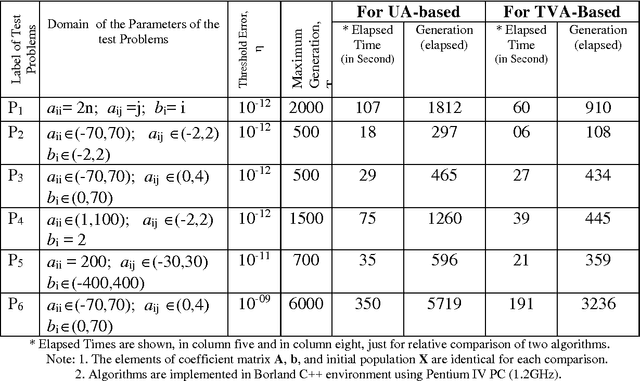
For small number of equations, systems of linear (and sometimes nonlinear) equations can be solved by simple classical techniques. However, for large number of systems of linear (or nonlinear) equations, solutions using classical method become arduous. On the other hand evolutionary algorithms have mostly been used to solve various optimization and learning problems. Recently, hybridization of evolutionary algorithm with classical Gauss-Seidel based Successive Over Relaxation (SOR) method has successfully been used to solve large number of linear equations; where a uniform adaptation (UA) technique of relaxation factor is used. In this paper, a new hybrid algorithm is proposed in which a time-variant adaptation (TVA) technique of relaxation factor is used instead of uniform adaptation technique to solve large number of linear equations. The convergence theorems of the proposed algorithms are proved theoretically. And the performance of the proposed TVA-based algorithm is compared with the UA-based hybrid algorithm in the experimental domain. The proposed algorithm outperforms the hybrid one in terms of efficiency.

Solving Linear Equations by Classical Jacobi-SR Based Hybrid Evolutionary Algorithm with Uniform Adaptation Technique

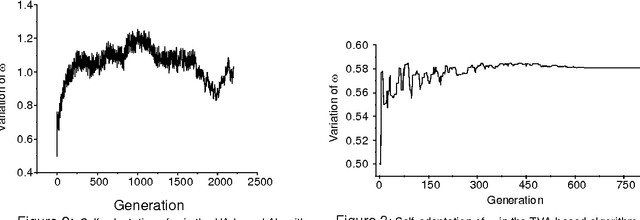
Solving a set of simultaneous linear equations is probably the most important topic in numerical methods. For solving linear equations, iterative methods are preferred over the direct methods especially when the coefficient matrix is sparse. The rate of convergence of iteration method is increased by using Successive Relaxation (SR) technique. But SR technique is very much sensitive to relaxation factor, {\omega}. Recently, hybridization of classical Gauss-Seidel based successive relaxation technique with evolutionary computation techniques have successfully been used to solve large set of linear equations in which relaxation factors are self-adapted. In this paper, a new hybrid algorithm is proposed in which uniform adaptive evolutionary computation techniques and classical Jacobi based SR technique are used instead of classical Gauss-Seidel based SR technique. The proposed Jacobi-SR based uniform adaptive hybrid algorithm, inherently, can be implemented in parallel processing environment efficiently. Whereas Gauss-Seidel-SR based hybrid algorithms cannot be implemented in parallel computing environment efficiently. The convergence theorem and adaptation theorem of the proposed algorithm are proved theoretically. And the performance of the proposed Jacobi-SR based uniform adaptive hybrid evolutionary algorithm is compared with Gauss-Seidel-SR based uniform adaptive hybrid evolutionary algorithm as well as with both classical Jacobi-SR method and Gauss-Seidel-SR method in the experimental domain. The proposed Jacobi-SR based hybrid algorithm outperforms the Gauss-Seidel-SR based hybrid algorithm as well as both classical Jacobi-SR method and Gauss-Seidel-SR method in terms of convergence speed and effectiveness.