Solving Linear Equations Using a Jacobi Based Time-Variant Adaptive Hybrid Evolutionary Algorithm

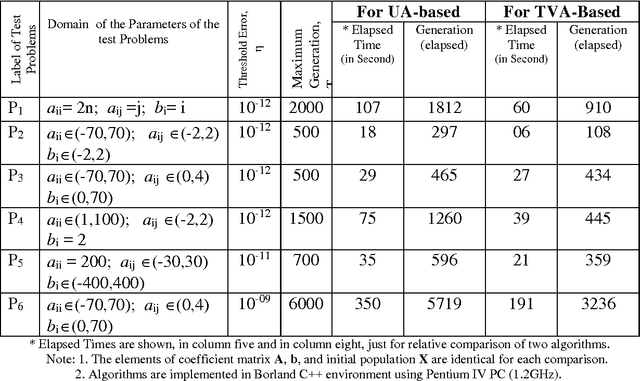
Large set of linear equations, especially for sparse and structured coefficient (matrix) equations, solutions using classical methods become arduous. And evolutionary algorithms have mostly been used to solve various optimization and learning problems. Recently, hybridization of classical methods (Jacobi method and Gauss-Seidel method) with evolutionary computation techniques have successfully been applied in linear equation solving. In the both above hybrid evolutionary methods, uniform adaptation (UA) techniques are used to adapt relaxation factor. In this paper, a new Jacobi Based Time-Variant Adaptive (JBTVA) hybrid evolutionary algorithm is proposed. In this algorithm, a Time-Variant Adaptive (TVA) technique of relaxation factor is introduced aiming at both improving the fine local tuning and reducing the disadvantage of uniform adaptation of relaxation factors. This algorithm integrates the Jacobi based SR method with time variant adaptive evolutionary algorithm. The convergence theorems of the proposed algorithm are proved theoretically. And the performance of the proposed algorithm is compared with JBUA hybrid evolutionary algorithm and classical methods in the experimental domain. The proposed algorithm outperforms both the JBUA hybrid algorithm and classical methods in terms of convergence speed and effectiveness.

An Approach to Solve Linear Equations Using a Time-Variant Adaptation Based Hybrid Evolutionary Algorithm

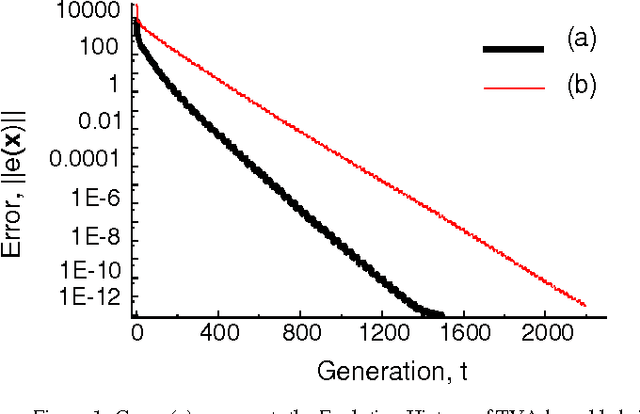
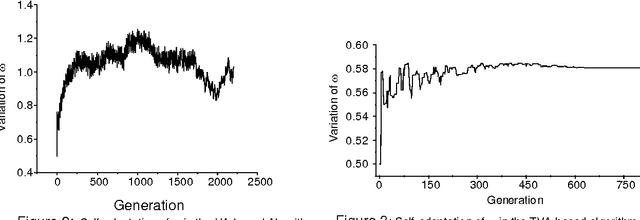
For small number of equations, systems of linear (and sometimes nonlinear) equations can be solved by simple classical techniques. However, for large number of systems of linear (or nonlinear) equations, solutions using classical method become arduous. On the other hand evolutionary algorithms have mostly been used to solve various optimization and learning problems. Recently, hybridization of evolutionary algorithm with classical Gauss-Seidel based Successive Over Relaxation (SOR) method has successfully been used to solve large number of linear equations; where a uniform adaptation (UA) technique of relaxation factor is used. In this paper, a new hybrid algorithm is proposed in which a time-variant adaptation (TVA) technique of relaxation factor is used instead of uniform adaptation technique to solve large number of linear equations. The convergence theorems of the proposed algorithms are proved theoretically. And the performance of the proposed TVA-based algorithm is compared with the UA-based hybrid algorithm in the experimental domain. The proposed algorithm outperforms the hybrid one in terms of efficiency.

For Solving Linear Equations Recombination is a Needless Operation in Time-Variant Adaptive Hybrid Algorithms

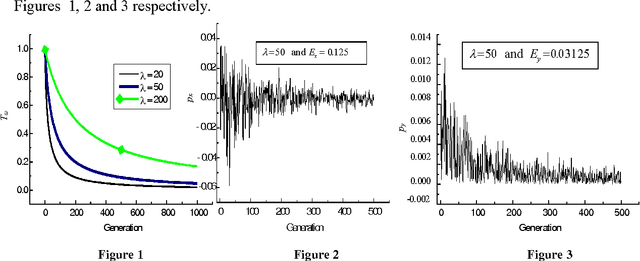
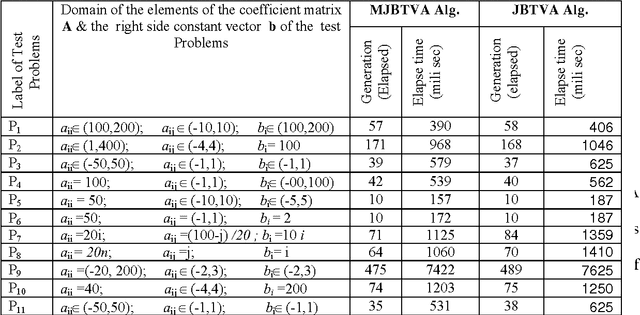
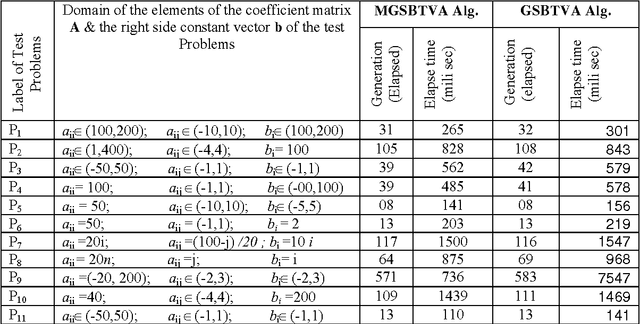
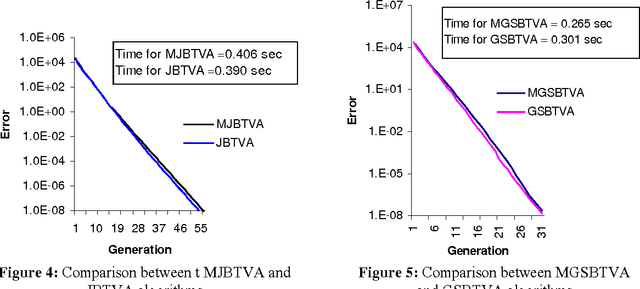
Recently hybrid evolutionary computation (EC) techniques are successfully implemented for solving large sets of linear equations. All the recently developed hybrid evolutionary algorithms, for solving linear equations, contain both the recombination and the mutation operations. In this paper, two modified hybrid evolutionary algorithms contained time-variant adaptive evolutionary technique are proposed for solving linear equations in which recombination operation is absent. The effectiveness of the recombination operator has been studied for the time-variant adaptive hybrid algorithms for solving large set of linear equations. Several experiments have been carried out using both the proposed modified hybrid evolutionary algorithms (in which the recombination operation is absent) and corresponding existing hybrid algorithms (in which the recombination operation is present) to solve large set of linear equations. It is found that the number of generations required by the existing hybrid algorithms (i.e. the Gauss-Seidel-SR based time variant adaptive (GSBTVA) hybrid algorithm and the Jacobi-SR based time variant adaptive (JBTVA) hybrid algorithm) and modified hybrid algorithms (i.e. the modified Gauss-Seidel-SR based time variant adaptive (MGSBTVA) hybrid algorithm and the modified Jacobi-SR based time variant adaptive (MJBTVA) hybrid algorithm) are comparable. Also the proposed modified algorithms require less amount of computational time in comparison to the corresponding existing hybrid algorithms. As the proposed modified hybrid algorithms do not contain recombination operation, so they require less computational effort, and also they are more efficient, effective and easy to implement.