Range-based argumentation semantics as 2-valued models

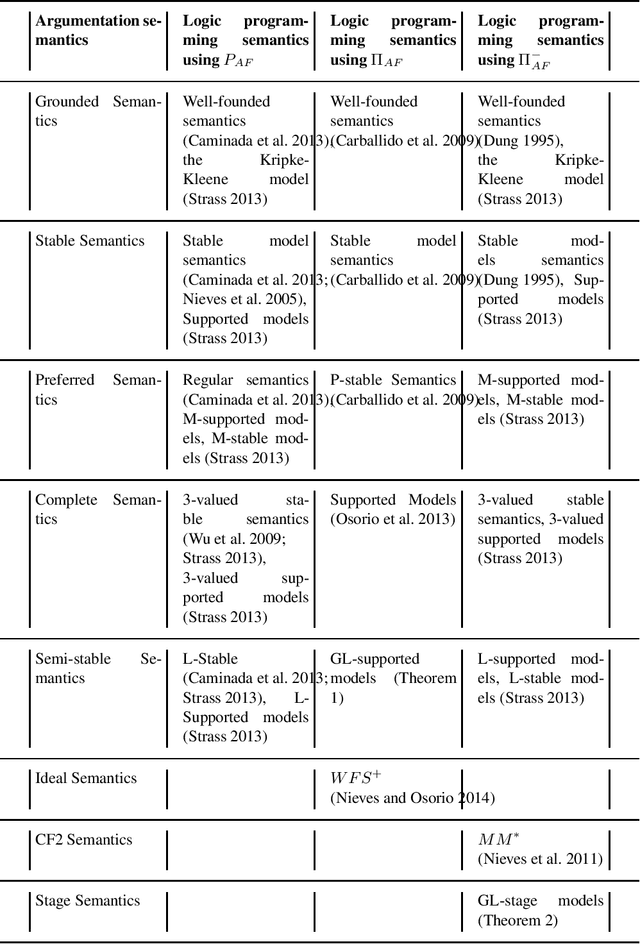
Characterizations of semi-stable and stage extensions in terms of 2-valued logical models are presented. To this end, the so-called GL-supported and GL-stage models are defined. These two classes of logical models are logic programming counterparts of the notion of range which is an established concept in argumentation semantics.

Semantics for Possibilistic Disjunctive Programs

In this paper, a possibilistic disjunctive logic programming approach for modeling uncertain, incomplete and inconsistent information is defined. This approach introduces the use of possibilistic disjunctive clauses which are able to capture incomplete information and incomplete states of a knowledge base at the same time. By considering a possibilistic logic program as a possibilistic logic theory, a construction of a possibilistic logic programming semantic based on answer sets and the proof theory of possibilistic logic is defined. It shows that this possibilistic semantics for disjunctive logic programs can be characterized by a fixed-point operator. It is also shown that the suggested possibilistic semantics can be computed by a resolution algorithm and the consideration of optimal refutations from a possibilistic logic theory. In order to manage inconsistent possibilistic logic programs, a preference criterion between inconsistent possibilistic models is defined; in addition, the approach of cuts for restoring consistency of an inconsistent possibilistic knowledge base is adopted. The approach is illustrated in a medical scenario.

Preferred extensions as stable models

Given an argumentation framework AF, we introduce a mapping function that constructs a disjunctive logic program P, such that the preferred extensions of AF correspond to the stable models of P, after intersecting each stable model with the relevant atoms. The given mapping function is of polynomial size w.r.t. AF. In particular, we identify that there is a direct relationship between the minimal models of a propositional formula and the preferred extensions of an argumentation framework by working on representing the defeated arguments. Then we show how to infer the preferred extensions of an argumentation framework by using UNSAT algorithms and disjunctive stable model solvers. The relevance of this result is that we define a direct relationship between one of the most satisfactory argumentation semantics and one of the most successful approach of non-monotonic reasoning i.e., logic programming with the stable model semantics.