Deep Neural Networks with Efficient Guaranteed Invariances

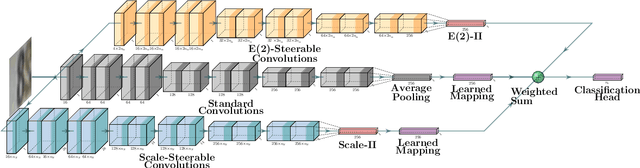
We address the problem of improving the performance and in particular the sample complexity of deep neural networks by enforcing and guaranteeing invariances to symmetry transformations rather than learning them from data. Group-equivariant convolutions are a popular approach to obtain equivariant representations. The desired corresponding invariance is then imposed using pooling operations. For rotations, it has been shown that using invariant integration instead of pooling further improves the sample complexity. In this contribution, we first expand invariant integration beyond rotations to flips and scale transformations. We then address the problem of incorporating multiple desired invariances into a single network. For this purpose, we propose a multi-stream architecture, where each stream is invariant to a different transformation such that the network can simultaneously benefit from multiple invariances. We demonstrate our approach with successful experiments on Scaled-MNIST, SVHN, CIFAR-10 and STL-10.

Improving the Sample-Complexity of Deep Classification Networks with Invariant Integration

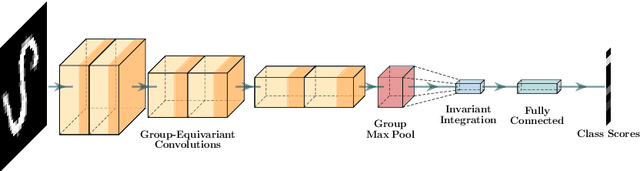
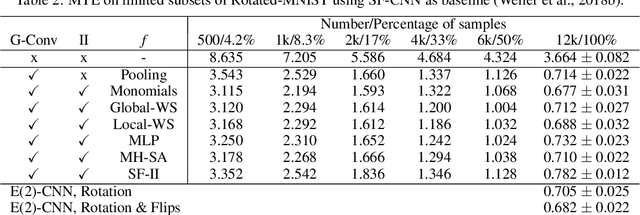
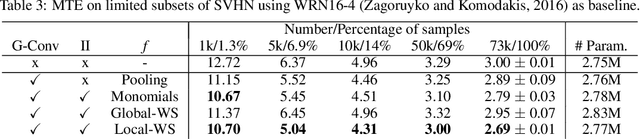
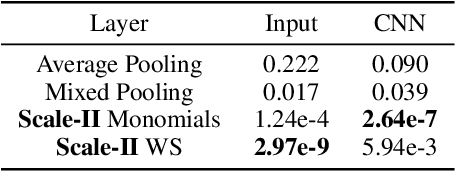
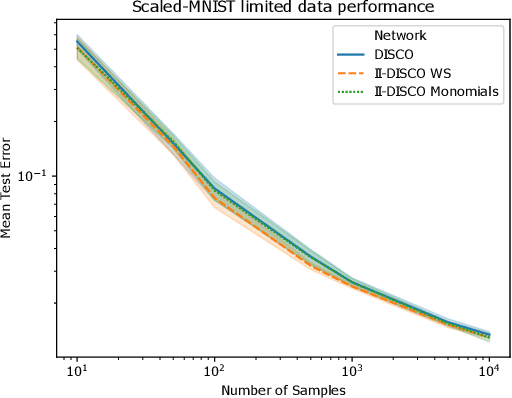
Leveraging prior knowledge on intraclass variance due to transformations is a powerful method to improve the sample complexity of deep neural networks. This makes them applicable to practically important use-cases where training data is scarce. Rather than being learned, this knowledge can be embedded by enforcing invariance to those transformations. Invariance can be imposed using group-equivariant convolutions followed by a pooling operation. For rotation-invariance, previous work investigated replacing the spatial pooling operation with invariant integration which explicitly constructs invariant representations. Invariant integration uses monomials which are selected using an iterative approach requiring expensive pre-training. We propose a novel monomial selection algorithm based on pruning methods to allow an application to more complex problems. Additionally, we replace monomials with different functions such as weighted sums, multi-layer perceptrons and self-attention, thereby streamlining the training of invariant-integration-based architectures. We demonstrate the improved sample complexity on the Rotated-MNIST, SVHN and CIFAR-10 datasets where rotation-invariant-integration-based Wide-ResNet architectures using monomials and weighted sums outperform the respective baselines in the limited sample regime. We achieve state-of-the-art results using full data on Rotated-MNIST and SVHN where rotation is a main source of intraclass variation. On STL-10 we outperform a standard and a rotation-equivariant convolutional neural network using pooling.

Boosting Deep Neural Networks with Geometrical Prior Knowledge: A Survey

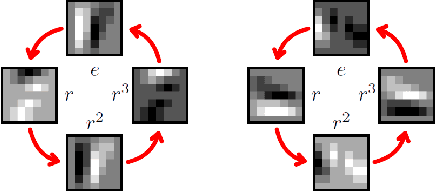
While Deep Neural Networks (DNNs) achieve state-of-the-art results in many different problem settings, they are affected by some crucial weaknesses. On the one hand, DNNs depend on exploiting a vast amount of training data, whose labeling process is time-consuming and expensive. On the other hand, DNNs are often treated as black box systems, which complicates their evaluation and validation. Both problems can be mitigated by incorporating prior knowledge into the DNN. One promising field, inspired by the success of convolutional neural networks (CNNs) in computer vision tasks, is to incorporate knowledge about symmetric geometrical transformations of the problem to solve. This promises an increased data-efficiency and filter responses that are interpretable more easily. In this survey, we try to give a concise overview about different approaches to incorporate geometrical prior knowledge into DNNs. Additionally, we try to connect those methods to the field of 3D object detection for autonomous driving, where we expect promising results applying those methods.

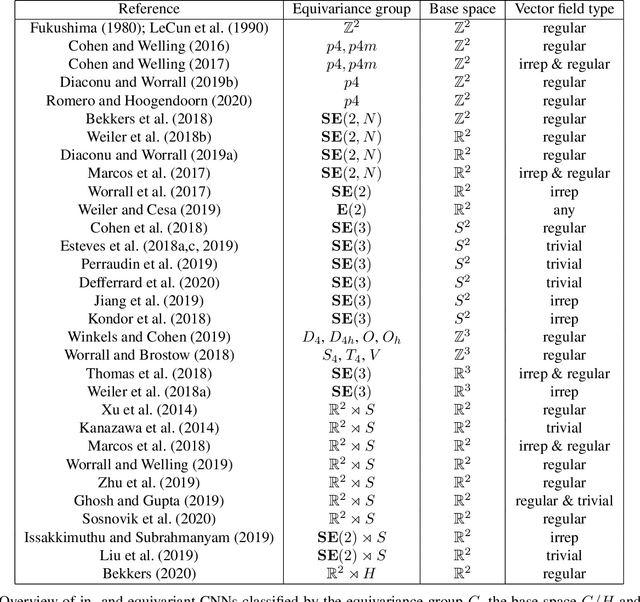
Invariant Integration in Deep Convolutional Feature Space

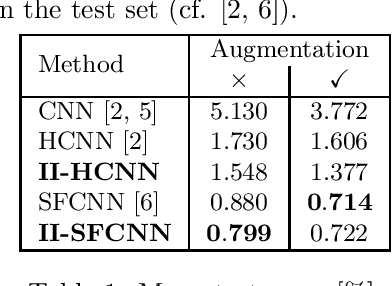
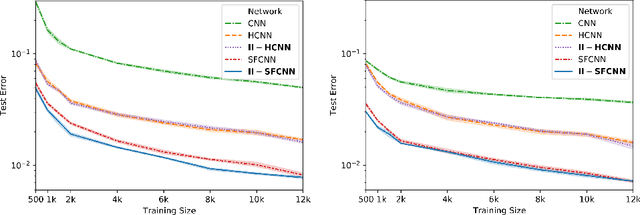
In this contribution, we show how to incorporate prior knowledge to a deep neural network architecture in a principled manner. We enforce feature space invariances using a novel layer based on invariant integration. This allows us to construct a complete feature space invariant to finite transformation groups. We apply our proposed layer to explicitly insert invariance properties for vision-related classification tasks, demonstrate our approach for the case of rotation invariance and report state-of-the-art performance on the Rotated-MNIST dataset. Our method is especially beneficial when training with limited data.