Matthias Lalisse
Distributed neural encoding of binding to thematic roles
Oct 24, 2021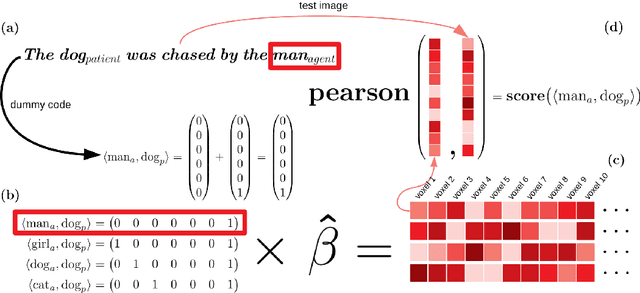

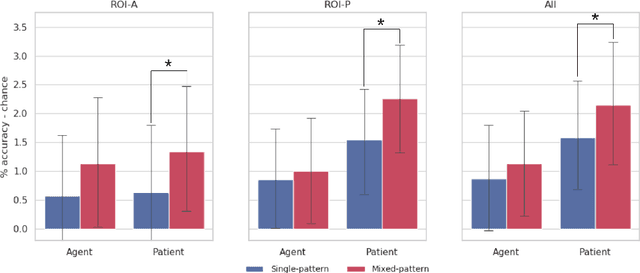

Abstract:A framework and method are proposed for the study of constituent composition in fMRI. The method produces estimates of neural patterns encoding complex linguistic structures, under the assumption that the contributions of individual constituents are additive. Like usual techniques for modeling compositional structure in fMRI, the proposed method employs pattern superposition to synthesize complex structures from their parts. Unlike these techniques, superpositions are sensitive to the structural positions of constituents, making them irreducible to structure-indiscriminate ("bag-of-words") models of composition. Reanalyzing data from a study by Frankland and Greene (2015), it is shown that comparison of neural predictive models with differing specifications can illuminate aspects of neural representational contents that are not apparent when composition is not modelled. The results indicate that the neural instantiations of the binding of fillers to thematic roles in a sentence are non-orthogonal, and therefore spatially overlapping.
Scalable knowledge base completion with superposition memories
Oct 24, 2021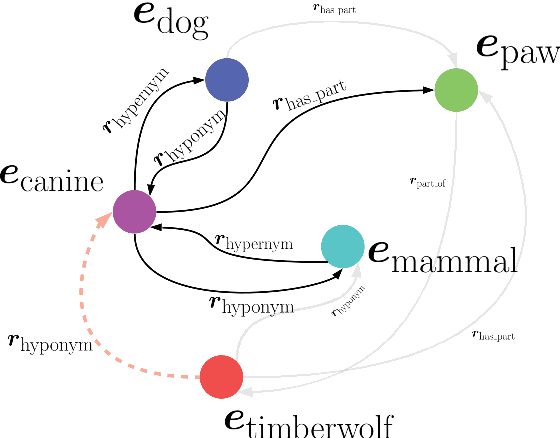
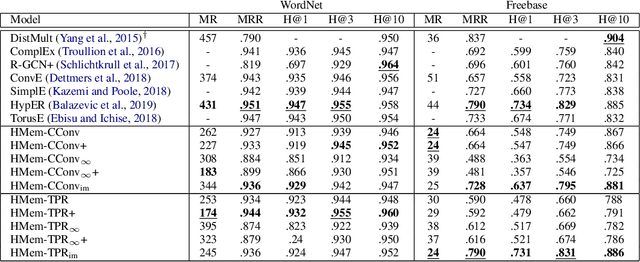
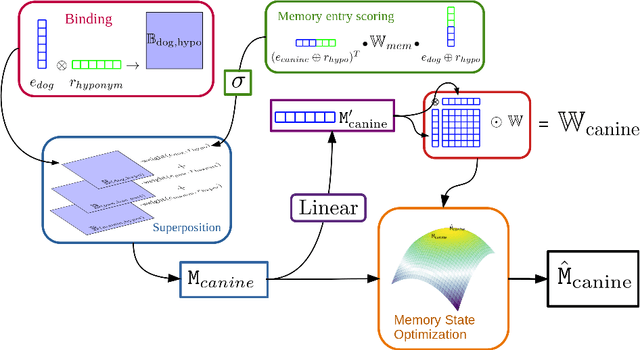
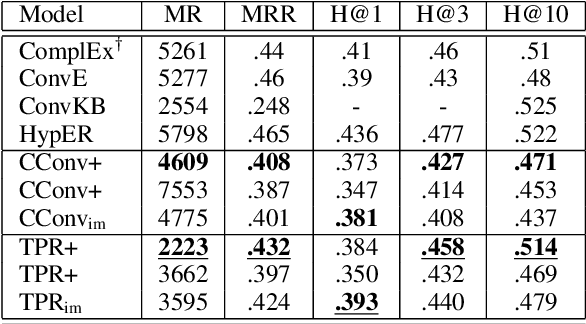
Abstract:We present Harmonic Memory Networks (HMem), a neural architecture for knowledge base completion that models entities as weighted sums of pairwise bindings between an entity's neighbors and corresponding relations. Since entities are modeled as aggregated neighborhoods, representations of unseen entities can be generated on the fly. We demonstrate this with two new datasets: WNGen and FBGen. Experiments show that the model is SOTA on benchmarks, and flexible enough to evolve without retraining as the knowledge graph grows.
Augmenting Compositional Models for Knowledge Base Completion Using Gradient Representations
Nov 02, 2018



Abstract:Neural models of Knowledge Base data have typically employed compositional representations of graph objects: entity and relation embeddings are systematically combined to evaluate the truth of a candidate Knowedge Base entry. Using a model inspired by Harmonic Grammar, we propose to tokenize triplet embeddings by subjecting them to a process of optimization with respect to learned well-formedness conditions on Knowledge Base triplets. The resulting model, known as Gradient Graphs, leads to sizable improvements when implemented as a companion to compositional models. Also, we show that the "supracompositional" triplet token embeddings it produces have interpretable properties that prove helpful in performing inference on the resulting triplet representations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge