Matthew S. Turner
Learning to swim efficiently in a nonuniform flow field
Dec 22, 2022Abstract:Microswimmers can acquire information on the surrounding fluid by sensing mechanical queues. They can then navigate in response to these signals. We analyse this navigation by combining deep reinforcement learning with direct numerical simulations to resolve the hydrodynamics. We study how local and non-local information can be used to train a swimmer to achieve particular swimming tasks in a non-uniform flow field, in particular a zig-zag shear flow. The swimming tasks are (1) learning how to swim in the vorticity direction, (2) the shear-gradient direction, and (3) the shear flow direction. We find that access to lab frame information on the swimmer's instantaneous orientation is all that is required in order to reach the optimal policy for (1,2). However, information on both the translational and rotational velocities seem to be required to achieve (3). Inspired by biological microorganisms we also consider the case where the swimmers sense local information, i.e. surface hydrodynamic forces, together with a signal direction. This might correspond to gravity or, for micro-organisms with light sensors, a light source. In this case, we show that the swimmer can reach a comparable level of performance as a swimmer with access to lab frame variables. We also analyse the role of different swimming modes, i.e. pusher, puller, and neutral swimmers.
Nash Neural Networks : Inferring Utilities from Optimal Behaviour
Mar 25, 2022
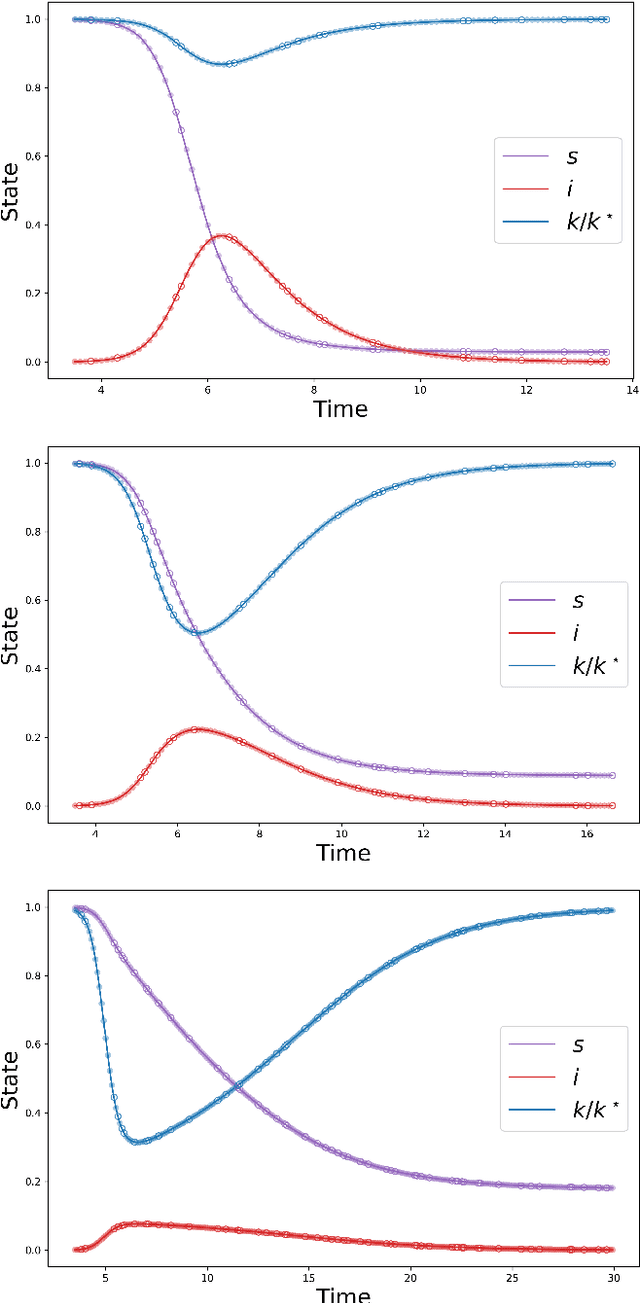
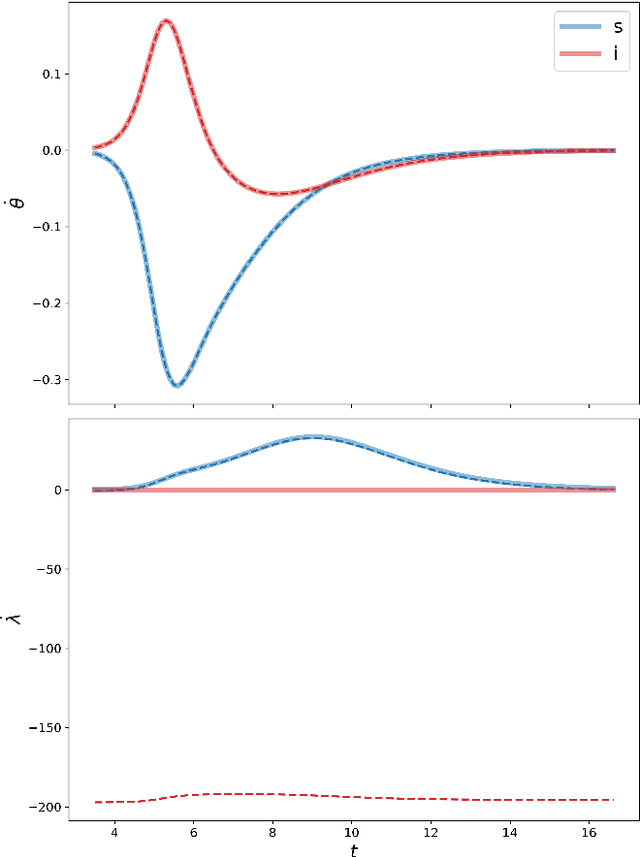

Abstract:We propose Nash Neural Networks ($N^3$) as a new type of Physics Informed Neural Network that is able to infer the underlying utility from observations of how rational individuals behave in a differential game with a Nash equilibrium. We assume that the dynamics for both the population and the individual are known, but not the payoff function, which specifies the cost per unit time of being in any particular state. We construct our network in such a way that the Euler-Lagrange equations of the corresponding optimal control problem are satisfied and the optimal control is self-consistently determined. In this way, we are able to learn the unknown payoff function in an unsupervised manner. We have applied the $N^3$ to study the optimal behaviour during epidemics, in which individuals can choose to socially distance depending on the state of the pandemic and the cost of being infected. Training our network against synthetic data for a simple SIR model, we showed that it is possible to accurately reproduce the hidden payoff function, in such a way that the game dynamics are respected. Our approach will have far-reaching applications, as it allows one to infer utilities from behavioural data, and can thus be applied to study a wide array of problems in science, engineering, economics and government planning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge