Matthew McAteer
BitTensor: An Intermodel Intelligence Measure
Mar 09, 2020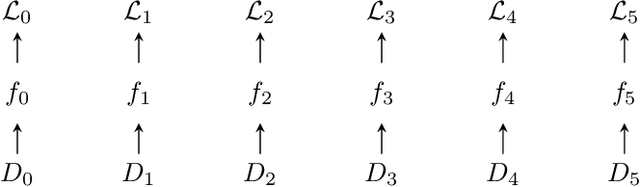
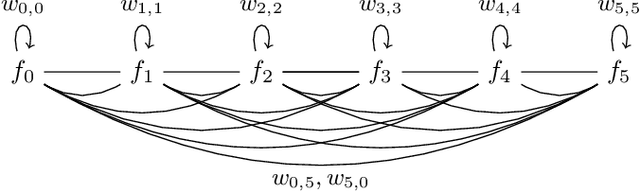
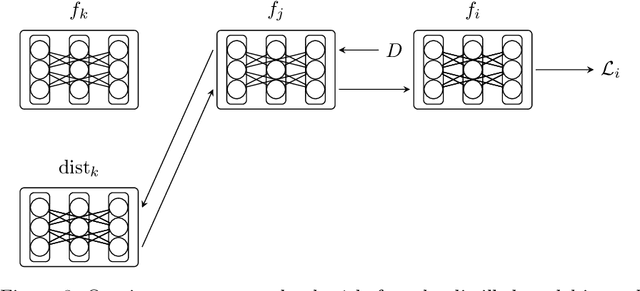
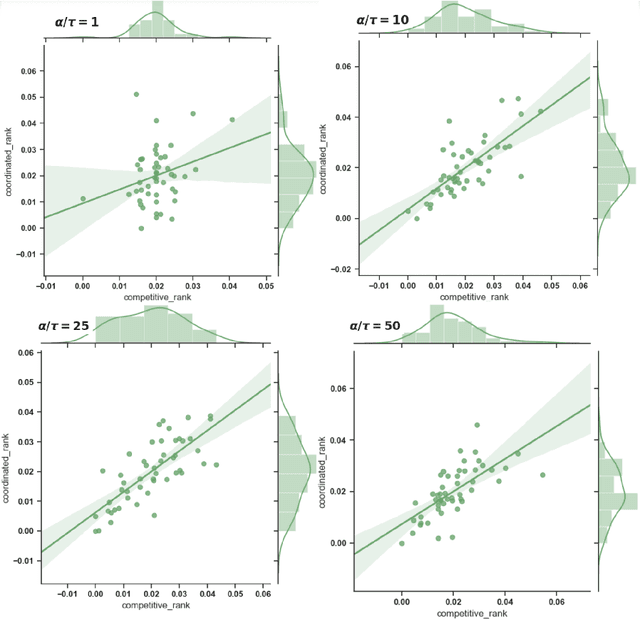
Abstract:A purely inter-model version of a machine intelligence benchmark would allow us to measure intelligence directly as information without projecting that information onto labeled datasets. We propose a framework in which other learners measure the informational significance of their peers across a network and use a digital ledger to negotiate the scores. However, the main benefits of measuring intelligence with other learners are lost if the underlying scores are dishonest. As a solution, we show how competition for connectivity in the network can be used to force honest bidding. We first prove that selecting inter-model scores using gradient descent is a regret-free strategy: one which generates the best subjective outcome regardless of the behavior of others. We then empirically show that when nodes apply this strategy, the network converges to a ranking that correlates with the one found in a fully coordinated and centralized setting. The result is a fair mechanism for training an internet-wide, decentralized and incentivized machine learning system, one which produces a continually hardening and expanding benchmark at the generalized intersection of the participants.
Model Weight Theft With Just Noise Inputs: The Curious Case of the Petulant Attacker
Dec 19, 2019



Abstract:This paper explores the scenarios under which an attacker can claim that 'Noise and access to the softmax layer of the model is all you need' to steal the weights of a convolutional neural network whose architecture is already known. We were able to achieve 96% test accuracy using the stolen MNIST model and 82% accuracy using the stolen KMNIST model learned using only i.i.d. Bernoulli noise inputs. We posit that this theft-susceptibility of the weights is indicative of the complexity of the dataset and propose a new metric that captures the same. The goal of this dissemination is to not just showcase how far knowing the architecture can take you in terms of model stealing, but to also draw attention to this rather idiosyncratic weight learnability aspects of CNNs spurred by i.i.d. noise input. We also disseminate some initial results obtained with using the Ising probability distribution in lieu of the i.i.d. Bernoulli distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge