Matthew Eaton
A Kronecker product accelerated efficient sparse Gaussian Process (E-SGP) for flow emulation
Dec 13, 2023



Abstract:In this paper, we introduce an efficient sparse Gaussian process (E-SGP) for the surrogate modelling of fluid mechanics. This novel Bayesian machine learning algorithm allows efficient model training using databases of different structures. It is a further development of the approximated sparse GP algorithm, combining the concept of efficient GP (E-GP) and variational energy free sparse Gaussian process (VEF-SGP). The developed E-SGP approach exploits the arbitrariness of inducing points and the monotonically increasing nature of the objective function with respect to the number of inducing points in VEF-SGP. By specifying the inducing points on the orthogonal grid/input subspace and using the Kronecker product, E-SGP significantly improves computational efficiency without imposing any constraints on the covariance matrix or increasing the number of parameters that need to be optimised during training. The E-SGP algorithm developed in this paper outperforms E-GP not only in scalability but also in model quality in terms of mean standardized logarithmic loss (MSLL). The computational complexity of E-GP suffers from the cubic growth regarding the growing structured training database. However, E-SGP maintains computational efficiency whilst the resolution of the model, (i.e., the number of inducing points) remains fixed. The examples show that E-SGP produces more accurate predictions in comparison with E-GP when the model resolutions are similar in both. E-GP benefits from more training data but comes with higher computational demands, while E-SGP achieves a comparable level of accuracy but is more computationally efficient, making E-SGP a potentially preferable choice for fluid mechanic problems. Furthermore, E-SGP can produce more reasonable estimates of model uncertainty, whilst E-GP is more likely to produce over-confident predictions.
Fixed Inducing Points Online Bayesian Calibration for Computer Models with an Application to a Scale-Resolving CFD Simulation
Sep 15, 2020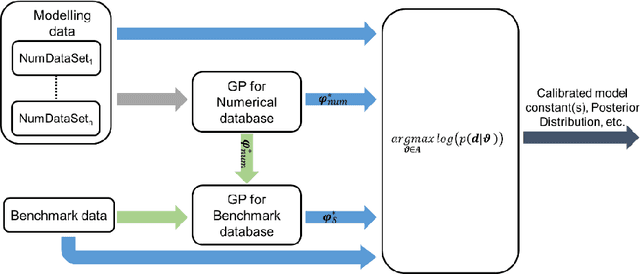
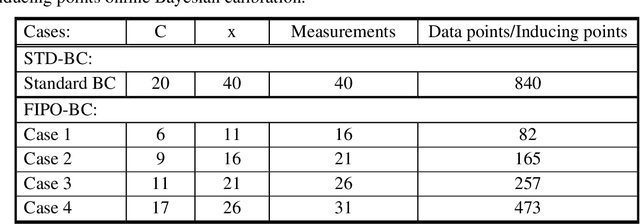
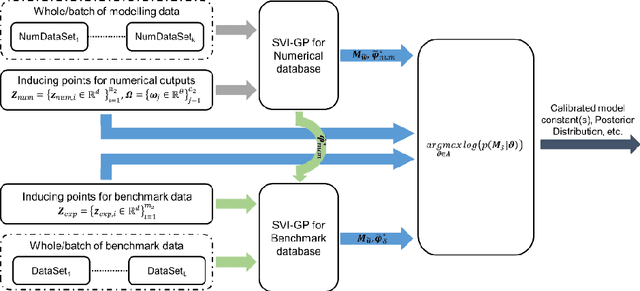
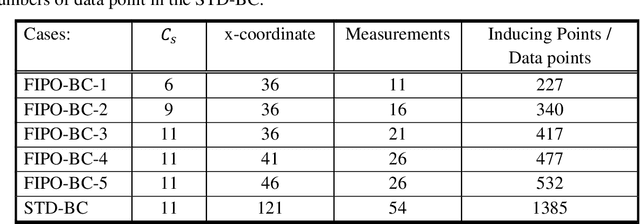
Abstract:This paper proposes a novel fixed inducing points online Bayesian calibration (FIPO-BC) algorithm to efficiently learn the model parameters using a benchmark database. The standard Bayesian calibration (STD-BC) algorithm provides a statistical method to calibrate the parameters of computationally expensive models. However, the STD-BC algorithm scales very badly with the number of data points and lacks online learning capability. The proposed FIPO-BC algorithm greatly improves the computational efficiency and enables the online calibration by executing the calibration on a set of predefined inducing points. To demonstrate the procedure of the FIPO-BC algorithm, two tests are performed, finding the optimal value and exploring the posterior distribution of 1) the parameter in a simple function, and 2) the high-wave number damping factor in a scale-resolving turbulence model (SAS-SST). The results (such as the calibrated model parameter and its posterior distribution) of FIPO-BC with different inducing points are compared to those of STD-BC. It is found that FIPO-BC and STD-BC can provide very similar results, once the predefined set of inducing point in FIPO-BC is sufficiently fine. But, the FIPO-BC algorithm is at least ten times faster than the STD-BC algorithm. Meanwhile, the online feature of the FIPO-BC allows continuous updating of the calibration outputs and potentially reduces the workload on generating the database.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge