Matias I. Müller
Asymptotically Optimal Bandits under Weighted Information
May 28, 2021
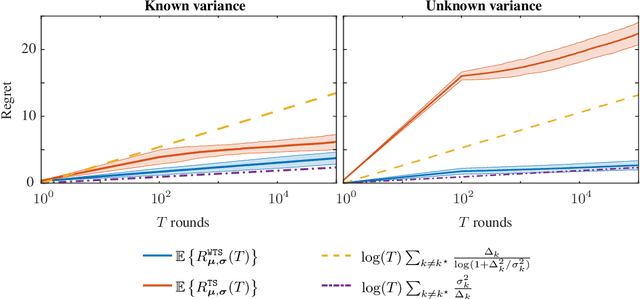
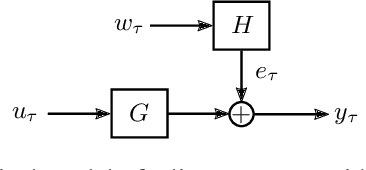
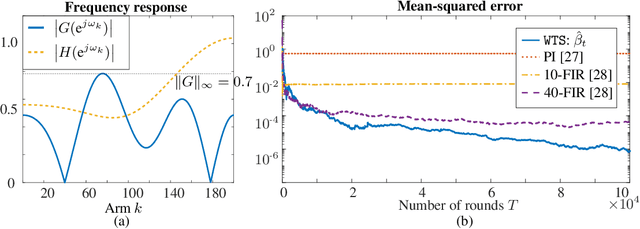
Abstract:We study the problem of regret minimization in a multi-armed bandit setup where the agent is allowed to play multiple arms at each round by spreading the resources usually allocated to only one arm. At each iteration the agent selects a normalized power profile and receives a Gaussian vector as outcome, where the unknown variance of each sample is inversely proportional to the power allocated to that arm. The reward corresponds to a linear combination of the power profile and the outcomes, resembling a linear bandit. By spreading the power, the agent can choose to collect information much faster than in a traditional multi-armed bandit at the price of reducing the accuracy of the samples. This setup is fundamentally different from that of a linear bandit -- the regret is known to scale as $\Theta(\sqrt{T})$ for linear bandits, while in this setup the agent receives a much more detailed feedback, for which we derive a tight $\log(T)$ problem-dependent lower-bound. We propose a Thompson-Sampling-based strategy, called Weighted Thompson Sampling (\WTS), that designs the power profile as its posterior belief of each arm being the best arm, and show that its upper bound matches the derived logarithmic lower bound. Finally, we apply this strategy to a problem of control and system identification, where the goal is to estimate the maximum gain (also called $\mathcal{H}_\infty$-norm) of a linear dynamical system based on batches of input-output samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge