Policy Optimization in Hybrid Discrete-Continuous Action Spaces via Mixed Gradients

We study reinforcement learning in hybrid discrete-continuous action spaces, such as settings where the discrete component selects a regime (or index) and the continuous component optimizes within it -- a structure common in robotics, control, and operations problems. Standard model-free policy gradient methods rely on score-function (SF) estimators and suffer from severe credit-assignment issues in high-dimensional settings, leading to poor gradient quality. On the other hand, differentiable simulation largely sidesteps these issues by backpropagating through a simulator, but the presence of discrete actions or non-smooth dynamics yields biased or uninformative gradients. To address this, we propose Hybrid Policy Optimization (HPO), which backpropagates through the simulator wherever smoothness permits, using a mixed gradient estimator that combines pathwise and SF gradients while maintaining unbiasedness. We also show how problems with action discontinuities can be reformulated in hybrid form, further broadening its applicability. Empirically, HPO substantially outperforms PPO on inventory control and switched linear-quadratic regulator problems, with performance gaps increasing as the continuous action dimension grows. Finally, we characterize the structure of the mixed gradient, showing that its cross term -- which captures how continuous actions influence future discrete decisions -- becomes negligible near a discrete best response, thereby enabling approximate decentralized updates of the continuous and discrete components and reducing variance near optimality. All resources are available at github.com/MatiasAlvo/hybrid-rl.

Neural Inventory Control in Networks via Hindsight Differentiable Policy Optimization

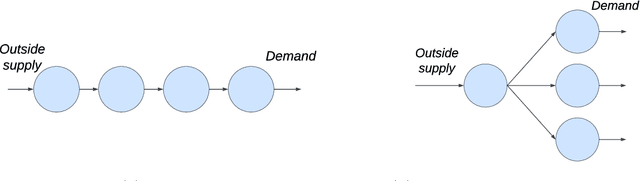
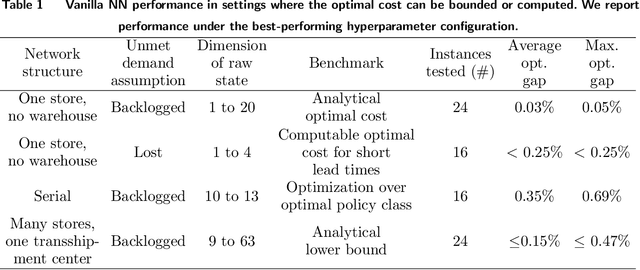
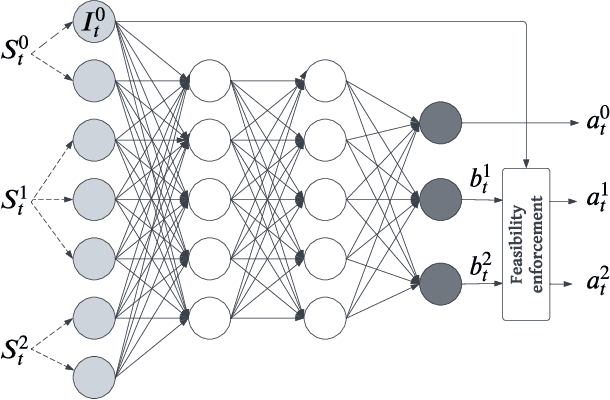
Inventory management offers unique opportunities for reliably evaluating and applying deep reinforcement learning (DRL). Rather than evaluate DRL algorithms by comparing against one another or against human experts, we can compare to the optimum itself in several problem classes with hidden structure. Our DRL methods consistently recover near-optimal policies in such settings, despite being applied with up to 600-dimensional raw state vectors. In others, they can vastly outperform problem-specific heuristics. To reliably apply DRL, we leverage two insights. First, one can directly optimize the hindsight performance of any policy using stochastic gradient descent. This uses (i) an ability to backtest any policy's performance on a subsample of historical demand observations, and (ii) the differentiability of the total cost incurred on any subsample with respect to policy parameters. Second, we propose a natural neural network architecture to address problems with weak (or aggregate) coupling constraints between locations in an inventory network. This architecture employs weight duplication for ``sibling'' locations in the network, and state summarization. We justify this architecture through an asymptotic guarantee, and empirically affirm its value in handling large-scale problems.