Matías Valdés
Re-Weighted $\ell_1$ Algorithms within the Lagrange Duality Framework: Bringing Interpretability to Weights
Jun 21, 2019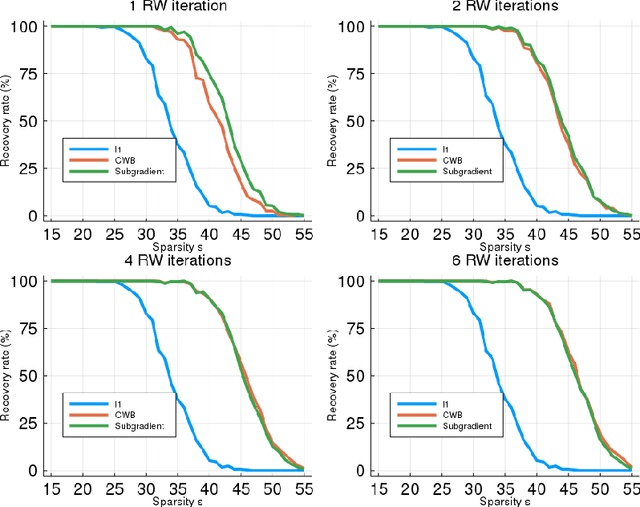
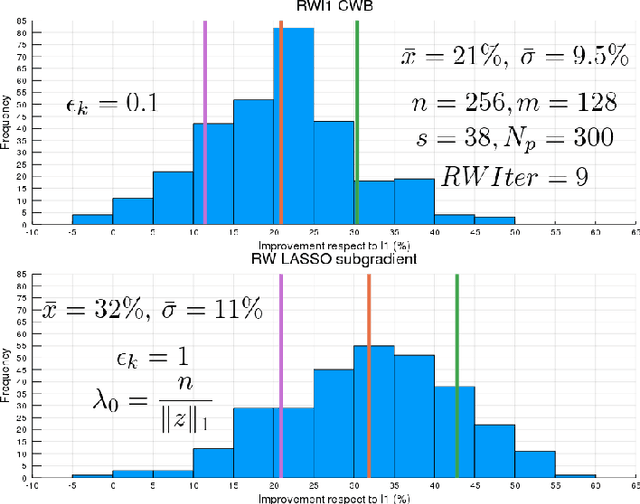
Abstract:We consider an important problem in signal processing, which consists in finding the sparsest solution of a linear system $\Phi x=b$. This problem has applications in several areas, but is NP-hard in general. Usually an alternative convex problem is considered, based on minimizing the (weighted) $\ell_{1}$ norm. For this alternative to be useful, weights should be chosen as to obtain a solution of the original NP-hard problem. A well known algorithm for this is the Re-Weighted $\ell_{1}$, proposed by Cand\`es, Wakin and Boyd. In this article we introduce a new methodology for updating the weights of a Re-Weighted $\ell_{1}$ algorithm, based on identifying these weights as Lagrange multipliers. This is then translated into an algorithm with performance comparable to the usual methodology, but allowing an interpretation of the weights as Lagrange multipliers. The methodology may also be used for a noisy linear system, obtaining in this case a Re-Weighted LASSO algorithm, with a promising performance according to the experimental results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge