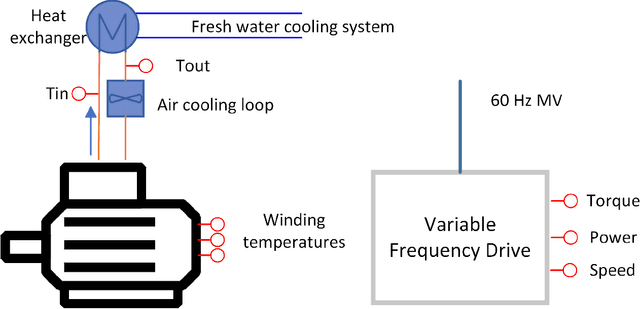
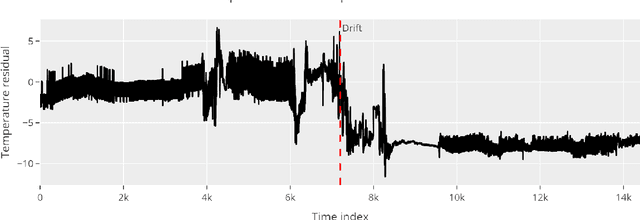
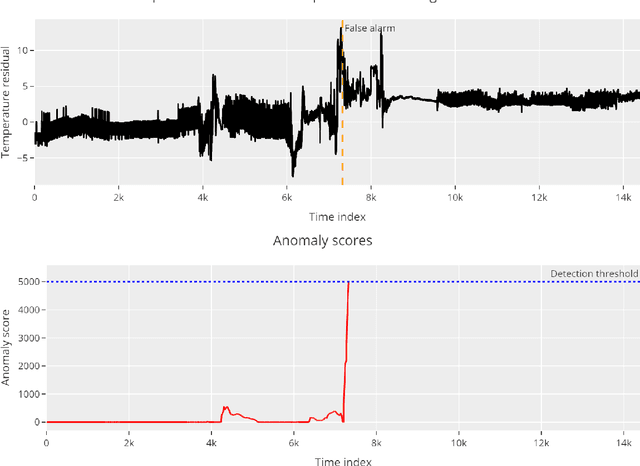
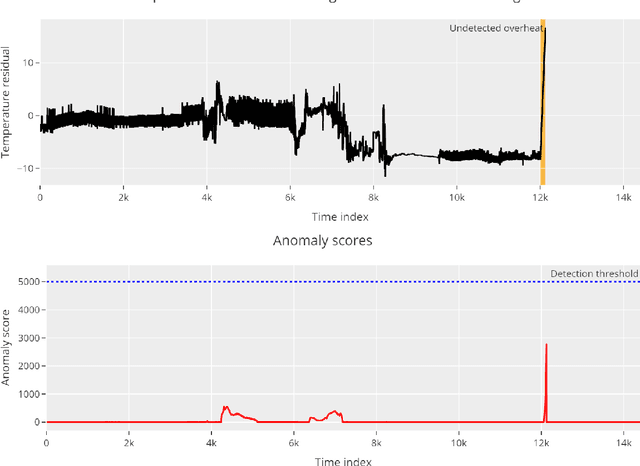
Fault detection in propulsion motors in the presence of concept drift

Machine learning and statistical methods can be used to enhance monitoring and fault prediction in marine systems. These methods rely on a dataset with records of historical system behaviour, potentially containing periods of both fault-free and faulty operation. An unexpected change in the underlying system, called a concept drift, may impact the performance of these methods, triggering the need for model retraining or other adaptations. In this article, we present an approach for detecting overheating in stator windings of marine propulsion motors that is able to successfully operate during concept drift without the need for full model retraining. Two distinct approaches are presented and tested. All models are trained and verified using a dataset from operational propulsion motors, with known, sudden concept drifts.

Online Detection of Sparse Changes in High-Dimensional Data Streams Using Tailored Projections

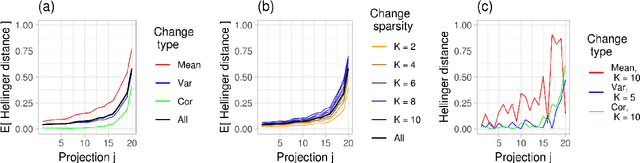
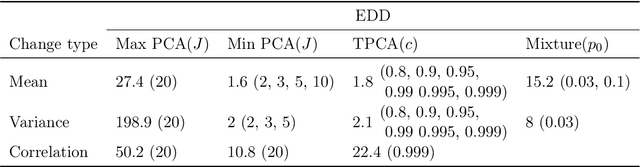
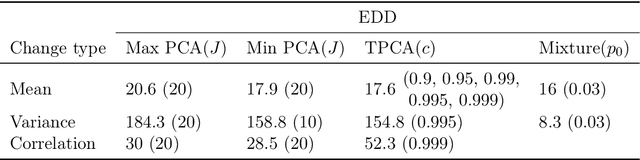
When applying principal component analysis (PCA) for dimension reduction, the most varying projections are usually used in order to retain most of the information. For the purpose of anomaly and change detection, however, the least varying projections are often the most important ones. In this article, we present a novel method that automatically tailors the choice of projections to monitor for sparse changes in the mean and/or covariance matrix of high-dimensional data. A subset of the least varying projections is almost always selected based on a criteria of the projection's sensitivity to changes. Our focus is on online/sequential change detection, where the aim is to detect changes as quickly as possible, while controlling false alarms at a specified level. A combination of tailored PCA and a generalized log-likelihood monitoring procedure displays high efficiency in detecting even very sparse changes in the mean, variance and correlation. We demonstrate on real data that tailored PCA monitoring is efficient for sparse change detection also when the data streams are highly auto-correlated and non-normal. Notably, error control is achieved without a large validation set, which is needed in most existing methods.

Which principal components are most sensitive to distributional changes?

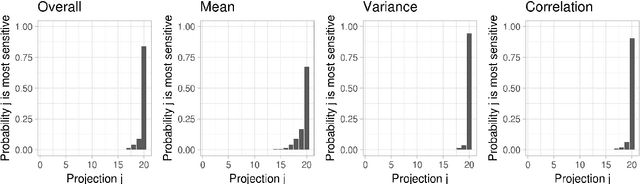
PCA is often used in anomaly detection and statistical process control tasks. For bivariate data, we prove that the minor projection (the least varying projection) of the PCA-rotated data is the most sensitive to distributional changes, where sensitivity is defined by the Hellinger distance between distributions before and after a change. In particular, this is almost always the case if only one parameter of the bivariate normal distribution changes, i.e., the change is sparse. Simulations indicate that the minor projections are the most sensitive for a large range of changes and pre-change settings in higher dimensions as well. This motivates using the minor projections for detecting sparse distributional changes in high-dimensional data.