Sampling and Update Frequencies in Proximal Variance Reduced Stochastic Gradient Methods

Variance reduced stochastic gradient methods have gained popularity in recent times. Several variants exist with different strategies for the storing and sampling of gradients. In this work we focus on the analysis of the interaction of these two aspects. We present and analyze a general proximal variance reduced gradient method under strong convexity assumptions. Special cases of the algorithm include SAGA, L-SVRG and their proximal variants. Our analysis sheds light on epoch-length selection and the need to balance the convergence of the iterates and how often gradients are stored. The analysis improves on other convergence rates found in literature and produces a new and faster converging sampling strategy for SAGA. Problem instances for which the predicted rates are the same as the practical rates are presented together with problems based on real world data.

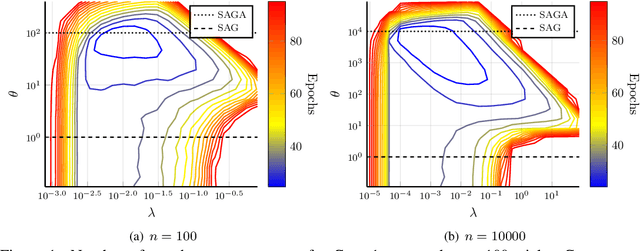
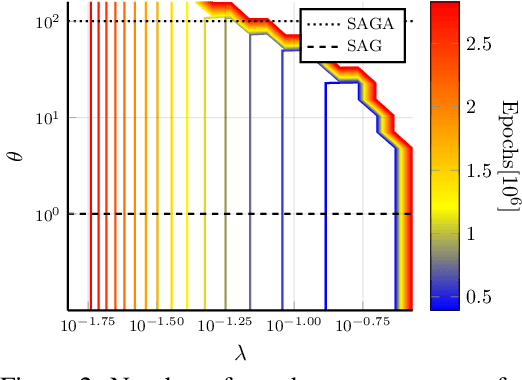
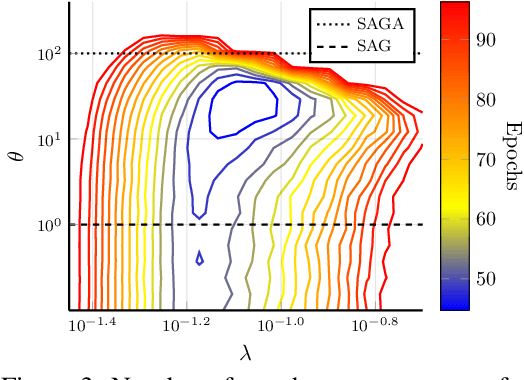
SVAG: Unified Convergence Results for SAG-SAGA Interpolation with Stochastic Variance Adjusted Gradient Descent

We analyze SVAG, a variance reduced stochastic gradient method with SAG and SAGA as special cases. Our convergence result for SVAG is the first to simultaneously capture both the biased low-variance method SAG and the unbiased high-variance method SAGA. In the case of SAGA, it matches previous upper bounds on the allowed step-size. The SVAG algorithm has a parameter that decides the bias-variance trade-off in the stochastic gradient estimate. We provide numerical examples demonstrating the intuition behind this bias-variance trade-off.