SVAG: Unified Convergence Results for SAG-SAGA Interpolation with Stochastic Variance Adjusted Gradient Descent
Paper and Code
Mar 21, 2019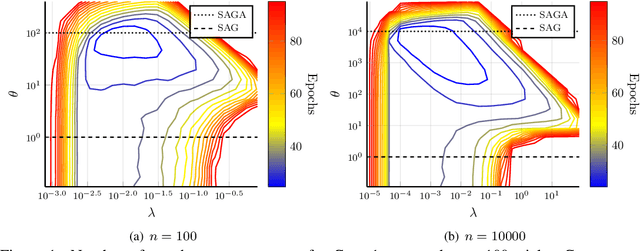
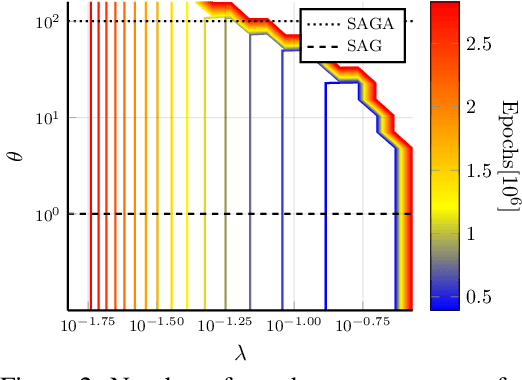
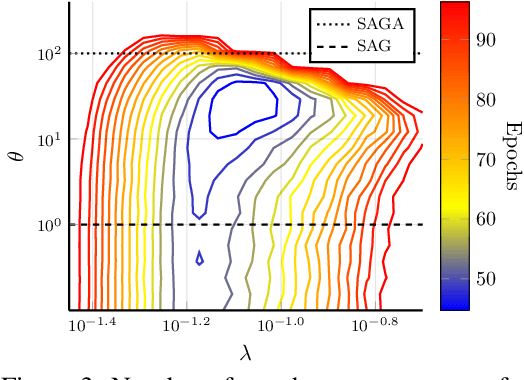
We analyze SVAG, a variance reduced stochastic gradient method with SAG and SAGA as special cases. Our convergence result for SVAG is the first to simultaneously capture both the biased low-variance method SAG and the unbiased high-variance method SAGA. In the case of SAGA, it matches previous upper bounds on the allowed step-size. The SVAG algorithm has a parameter that decides the bias-variance trade-off in the stochastic gradient estimate. We provide numerical examples demonstrating the intuition behind this bias-variance trade-off.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge