Marko V. Jankovic
A dual mode adaptive basal-bolus advisor based on reinforcement learning
Jan 07, 2019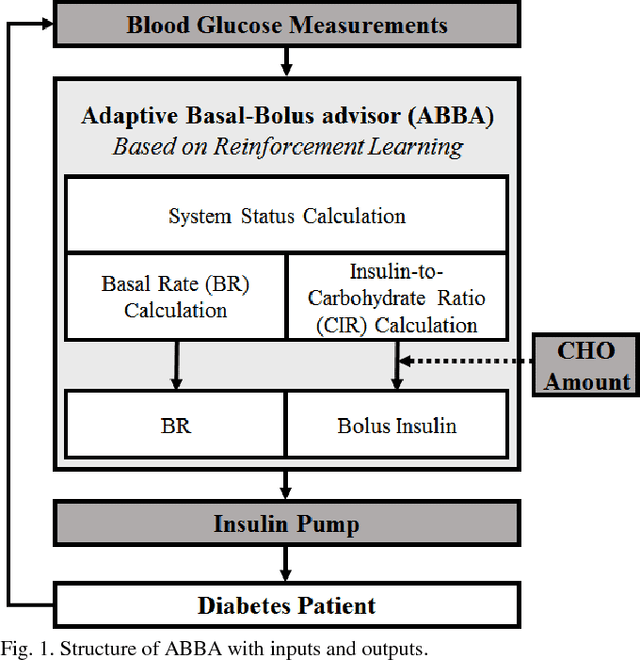
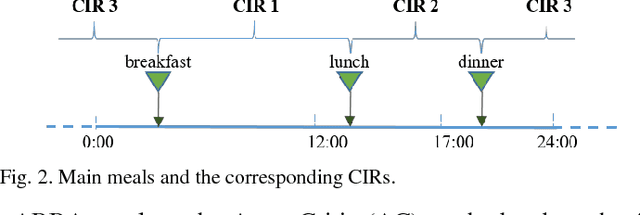

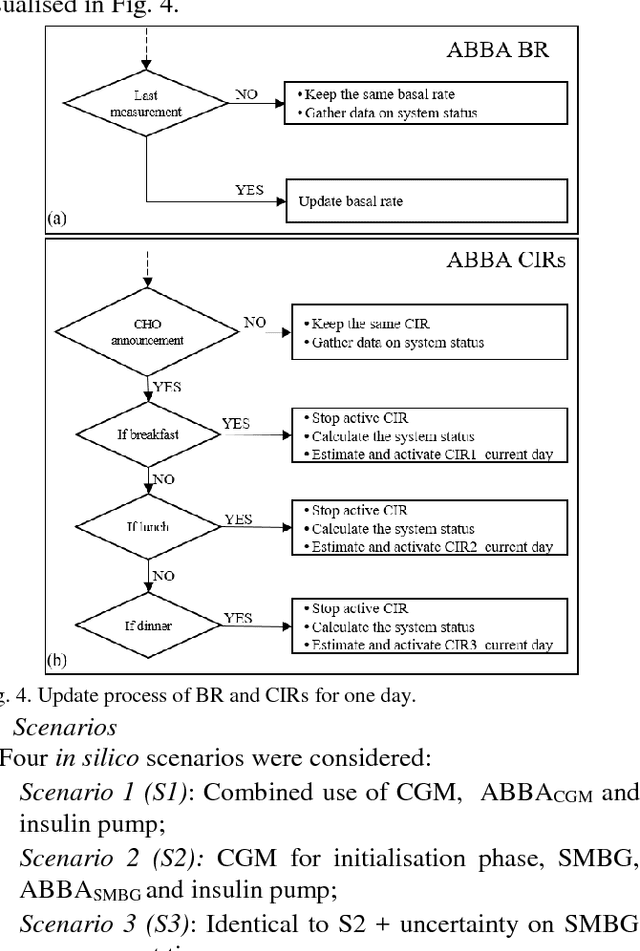
Abstract:Self-monitoring of blood glucose (SMBG) and continuous glucose monitoring (CGM) are commonly used by type 1 diabetes (T1D) patients to measure glucose concentrations. The proposed adaptive basal-bolus algorithm (ABBA) supports inputs from either SMBG or CGM devices to provide personalised suggestions for the daily basal rate and prandial insulin doses on the basis of the patients' glucose level on the previous day. The ABBA is based on reinforcement learning (RL), a type of artificial intelligence, and was validated in silico with an FDA-accepted population of 100 adults under different realistic scenarios lasting three simulated months. The scenarios involve three main meals and one bedtime snack per day, along with different variabilities and uncertainties for insulin sensitivity, mealtime, carbohydrate amount, and glucose measurement time. The results indicate that the proposed approach achieves comparable performance with CGM or SMBG as input signals, without influencing the total daily insulin dose. The results are a promising indication that AI algorithmic approaches can provide personalised adaptive insulin optimisation and achieve glucose control - independently of the type of glucose monitoring technology.
Predicting Blood Glucose with an LSTM and Bi-LSTM Based Deep Neural Network
Sep 11, 2018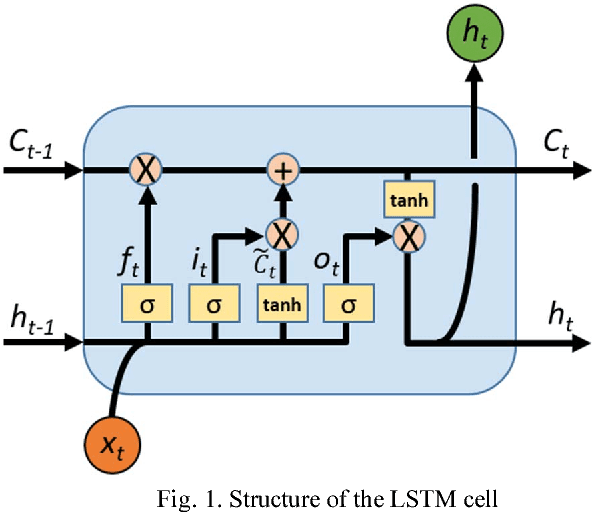
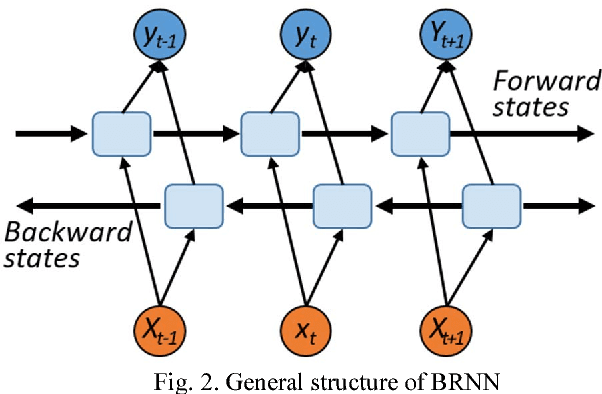
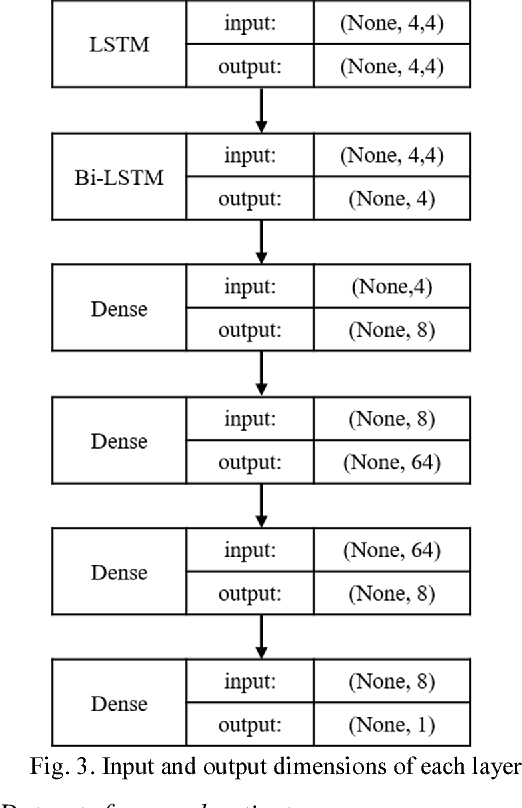
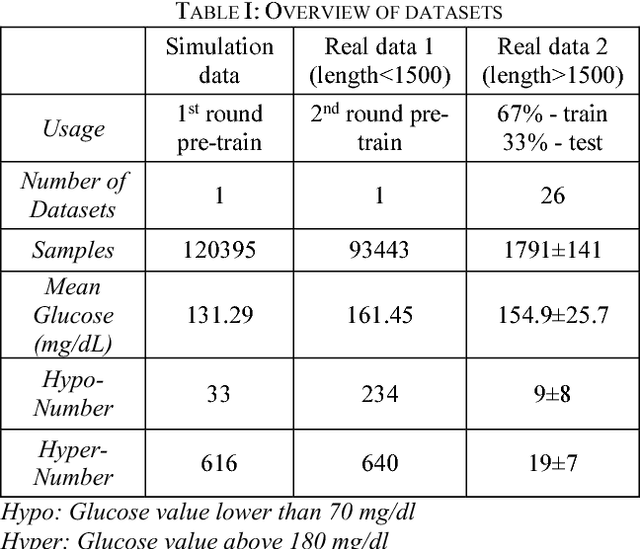
Abstract:A deep learning network was used to predict future blood glucose levels, as this can permit diabetes patients to take action before imminent hyperglycaemia and hypoglycaemia. A sequential model with one long-short-term memory (LSTM) layer, one bidirectional LSTM layer and several fully connected layers was used to predict blood glucose levels for different prediction horizons. The method was trained and tested on 26 datasets from 20 real patients. The proposed network outperforms the baseline methods in terms of all evaluation criteria.
Quantum Low Entropy based Associative Reasoning or QLEAR Learning
May 30, 2017
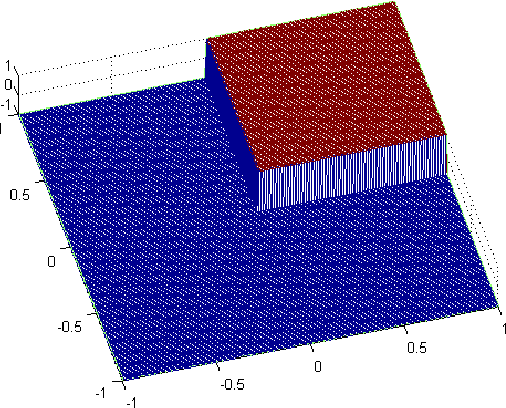
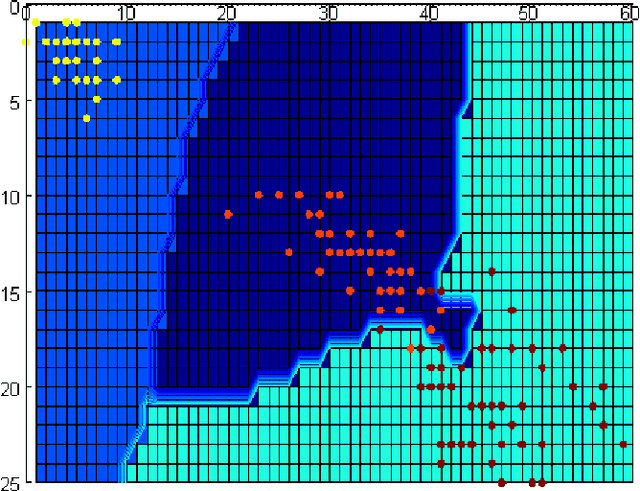

Abstract:In this paper, we propose the classification method based on a learning paradigm we are going to call Quantum Low Entropy based Associative Reasoning or QLEAR learning. The approach is based on the idea that classification can be understood as supervised clustering, where a quantum entropy in the context of the quantum probabilistic model, will be used as a "capturer" (measure, or external index), of the "natural structure" of the data. By using quantum entropy we do not make any assumption about linear separability of the data that are going to be classified. The basic idea is to find close neighbors to a query sample and then use relative change in the quantum entropy as a measure of similarity of the newly arrived sample with the representatives of interest. In other words, method is based on calculation of quantum entropy of the referent system and its relative change with the addition of the newly arrived sample. Referent system consists of vectors that represent individual classes and that are the most similar, in Euclidean distance sense, to the vector that is analyzed. Here, we analyze the classification problem in the context of measuring similarities to prototype examples of categories. While nearest neighbor classifiers are natural in this setting, they suffer from the problem of high variance (in bias-variance decomposition) in the case of limited sampling. Alternatively, one could use machine learning techniques (like support vector machines) but they involve time-consuming optimization. Here we propose a hybrid of nearest neighbor and machine learning technique which deals naturally with the multi-class setting, has reasonable computational complexity both in training and at run time, and yields excellent results in practice.
Probabilistic Approach to Neural Networks Computation Based on Quantum Probability Model Probabilistic Principal Subspace Analysis Example
Jan 25, 2010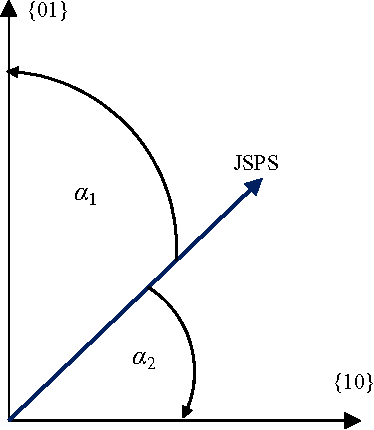
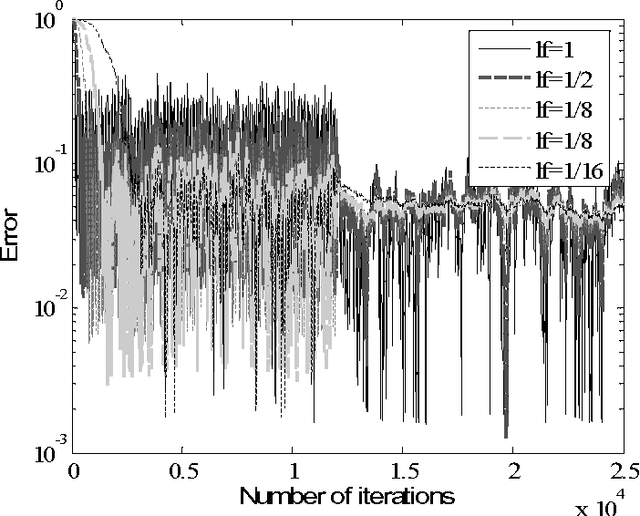
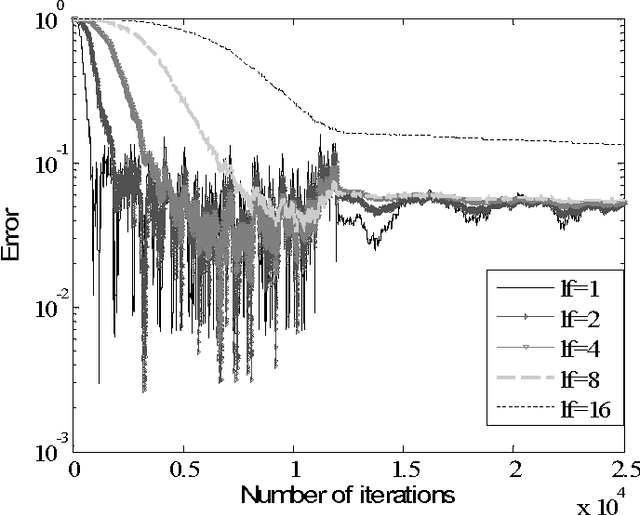
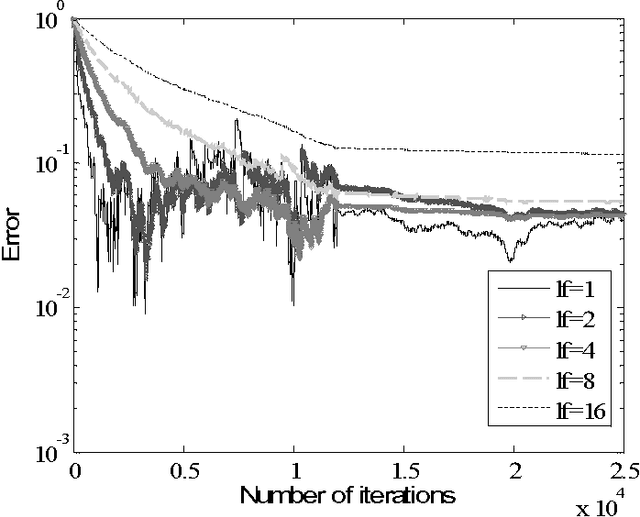
Abstract:In this paper, we introduce elements of probabilistic model that is suitable for modeling of learning algorithms in biologically plausible artificial neural networks framework. Model is based on two of the main concepts in quantum physics - a density matrix and the Born rule. As an example, we will show that proposed probabilistic interpretation is suitable for modeling of on-line learning algorithms for PSA, which are preferably realized by a parallel hardware based on very simple computational units. Proposed concept (model) can be used in the context of improving algorithm convergence speed, learning factor choice, or input signal scale robustness. We are going to see how the Born rule and the Hebbian learning rule are connected
Geometrical Interpretation of Shannon's Entropy Based on the Born Rule
Sep 28, 2009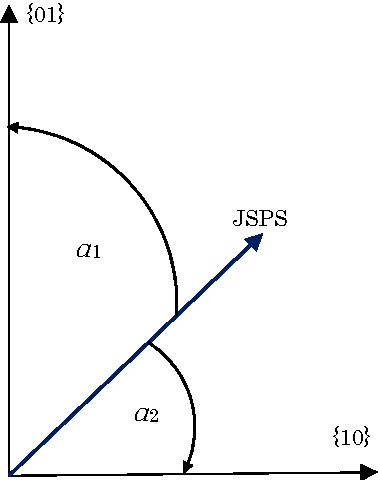
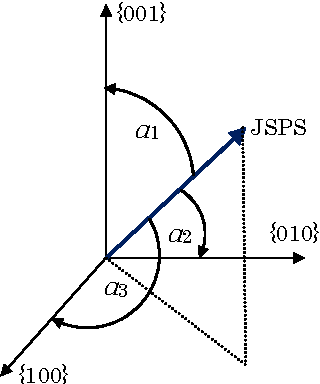
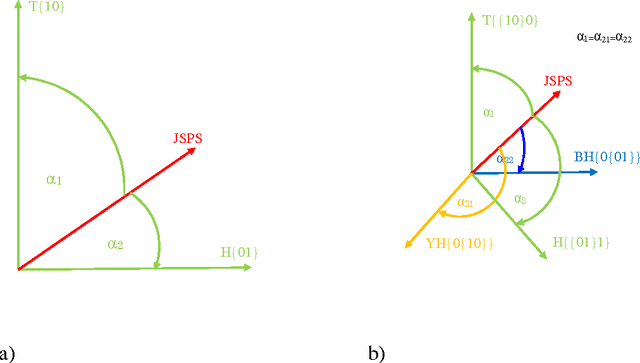
Abstract:In this paper we will analyze discrete probability distributions in which probabilities of particular outcomes of some experiment (microstates) can be represented by the ratio of natural numbers (in other words, probabilities are represented by digital numbers of finite representation length). We will introduce several results that are based on recently proposed JoyStick Probability Selector, which represents a geometrical interpretation of the probability based on the Born rule. The terms of generic space and generic dimension of the discrete distribution, as well as, effective dimension are going to be introduced. It will be shown how this simple geometric representation can lead to an optimal code length coding of the sequence of signals. Then, we will give a new, geometrical, interpretation of the Shannon entropy of the discrete distribution. We will suggest that the Shannon entropy represents the logarithm of the effective dimension of the distribution. Proposed geometrical interpretation of the Shannon entropy can be used to prove some information inequalities in an elementary way.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge