Geometrical Interpretation of Shannon's Entropy Based on the Born Rule
Paper and Code
Sep 28, 2009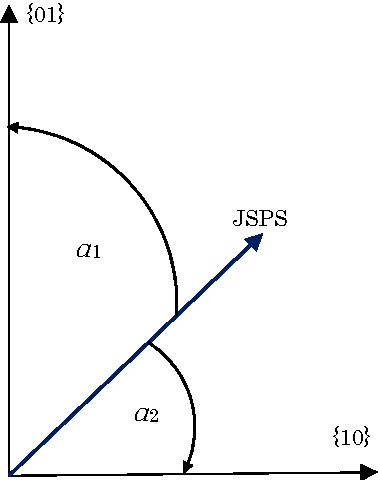
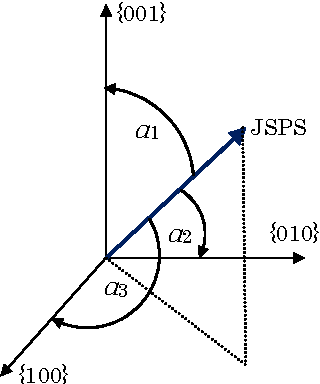
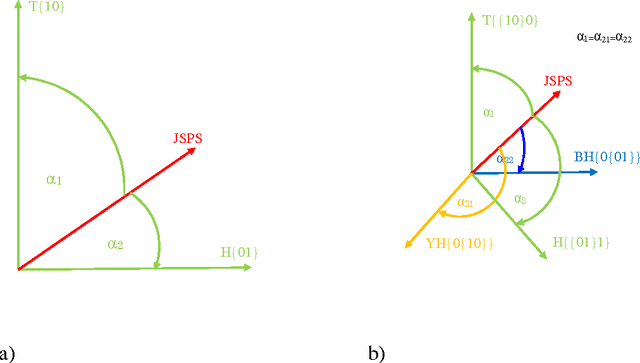
In this paper we will analyze discrete probability distributions in which probabilities of particular outcomes of some experiment (microstates) can be represented by the ratio of natural numbers (in other words, probabilities are represented by digital numbers of finite representation length). We will introduce several results that are based on recently proposed JoyStick Probability Selector, which represents a geometrical interpretation of the probability based on the Born rule. The terms of generic space and generic dimension of the discrete distribution, as well as, effective dimension are going to be introduced. It will be shown how this simple geometric representation can lead to an optimal code length coding of the sequence of signals. Then, we will give a new, geometrical, interpretation of the Shannon entropy of the discrete distribution. We will suggest that the Shannon entropy represents the logarithm of the effective dimension of the distribution. Proposed geometrical interpretation of the Shannon entropy can be used to prove some information inequalities in an elementary way.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge