Bayesian Optimization for Parameter Tuning of the XOR Neural Network

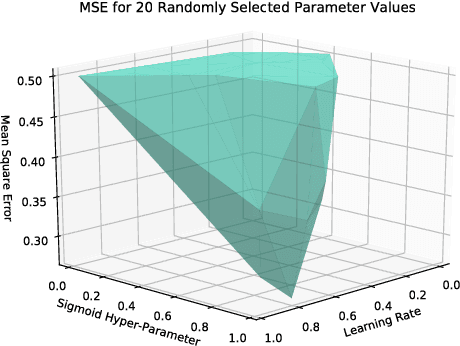
When applying Machine Learning techniques to problems, one must select model parameters to ensure that the system converges but also does not become stuck at the objective function's local minimum. Tuning these parameters becomes a non-trivial task for large models and it is not always apparent if the user has found the optimal parameters. We aim to automate the process of tuning a Neural Network, (where only a limited number of parameter search attempts are available) by implementing Bayesian Optimization. In particular, by assigning Gaussian Process Priors to the parameter space, we utilize Bayesian Optimization to tune an Artificial Neural Network used to learn the XOR function, with the result of achieving higher prediction accuracy.

Deriving Compact Laws Based on Algebraic Formulation of a Data Set

In various subjects, there exist compact and consistent relationships between input and output parameters. Discovering the relationships, or namely compact laws, in a data set is of great interest in many fields, such as physics, chemistry, and finance. While data discovery has made great progress in practice thanks to the success of machine learning in recent years, the development of analytical approaches in finding the theory behind the data is relatively slow. In this paper, we develop an innovative approach in discovering compact laws from a data set. By proposing a novel algebraic equation formulation, we convert the problem of deriving meaning from data into formulating a linear algebra model and searching for relationships that fit the data. Rigorous proof is presented in validating the approach. The algebraic formulation allows the search of equation candidates in an explicit mathematical manner. Searching algorithms are also proposed for finding the governing equations with improved efficiency. For a certain type of compact theory, our approach assures convergence and the discovery is computationally efficient and mathematically precise.