Response to Moffat's Comment on "Towards Meaningful Statements in IR Evaluation: Mapping Evaluation Measures to Interval Scales"

Moffat recently commented on our previous work. Our work focused on how laying the foundations of our evaluation methodology into the theory of measurement can improve our knowledge and understanding of the evaluation measures we use in IR and how it can shed light on the different types of scales adopted by our evaluation measures; we also provided evidence, through extensive experimentation, on the impact of the different types of scales on the statistical analyses, as well as on the impact of departing from their assumptions. Moreover, we investigated, for the first time in IR, the concept of meaningfulness, i.e. the invariance of the experimental statements and inferences you draw, and proposed it as a way to ensure more valid and generalizabile results. Moffat's comments build on: (i) misconceptions about the representational theory of measurement, such as what an interval scale actually is and what axioms it has to comply with; (ii) they totally miss the central concept of meaningfulness. Therefore, we reply to Moffat's comments by properly framing them in the representational theory of measurement and in the concept of meaningfulness. All in all, we can only reiterate what we said several times: the goal of this research line is to theoretically ground our evaluation methodology - and IR is a field where it is extremely challenging to perform any theoretical advances - in order to aim for more robust and generalizable inferences - something we currently lack in the field. Possibly there are other and better ways to achieve this objective and these proposals could emerge from an open discussion in the field and from the work of others. On the other hand, reducing everything to a contrast on what is (or pretend to be) an interval scale or whether all or none evaluation measures are interval scales may be more a barrier from than a help in progressing towards this goal.

Towards Meaningful Statements in IR Evaluation. Mapping Evaluation Measures to Interval Scales

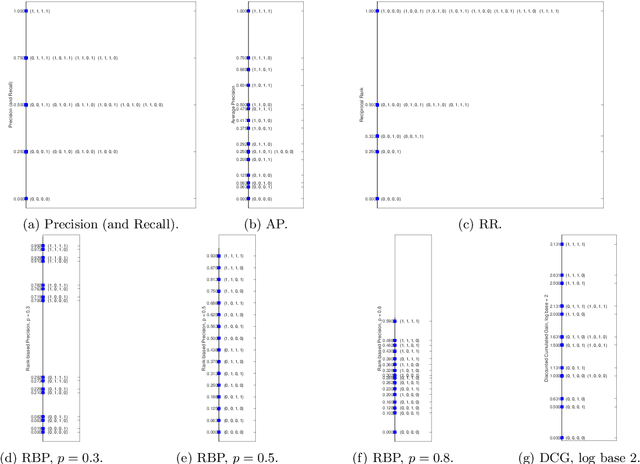
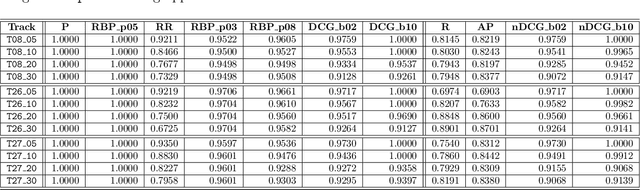
Recently, it was shown that most popular IR measures are not interval-scaled, implying that decades of experimental IR research used potentially improper methods, which may have produced questionable results. However, it was unclear if and to what extent these findings apply to actual evaluations and this opened a debate in the community with researchers standing on opposite positions about whether this should be considered an issue (or not) and to what extent. In this paper, we first give an introduction to the representational measurement theory explaining why certain operations and significance tests are permissible only with scales of a certain level. For that, we introduce the notion of meaningfulness specifying the conditions under which the truth (or falsity) of a statement is invariant under permissible transformations of a scale. Furthermore, we show how the recall base and the length of the run may make comparison and aggregation across topics problematic. Then we propose a straightforward and powerful approach for turning an evaluation measure into an interval scale, and describe an experimental evaluation of the differences between using the original measures and the interval-scaled ones. For all the regarded measures - namely Precision, Recall, Average Precision, (Normalized) Discounted Cumulative Gain, Rank-Biased Precision and Reciprocal Rank - we observe substantial effects, both on the order of average values and on the outcome of significance tests. For the latter, previously significant differences turn out to be insignificant, while insignificant ones become significant. The effect varies remarkably between the tests considered but overall, on average, we observed a 25% change in the decision about which systems are significantly different and which are not.