Cooperative versus decentralized strategies in three-pursuer single-evader games

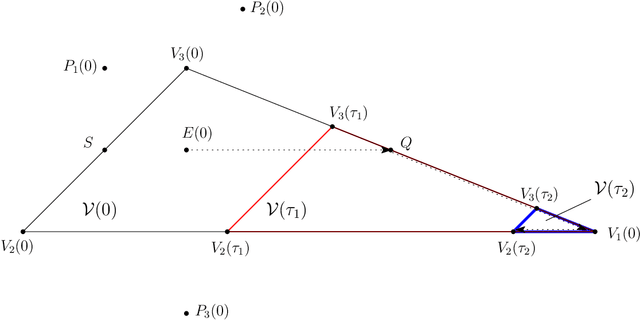
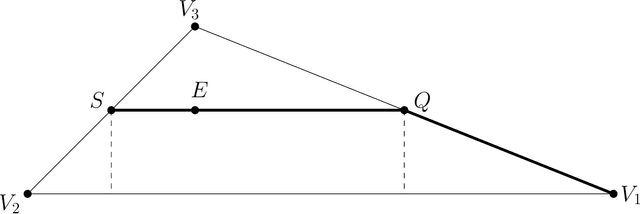
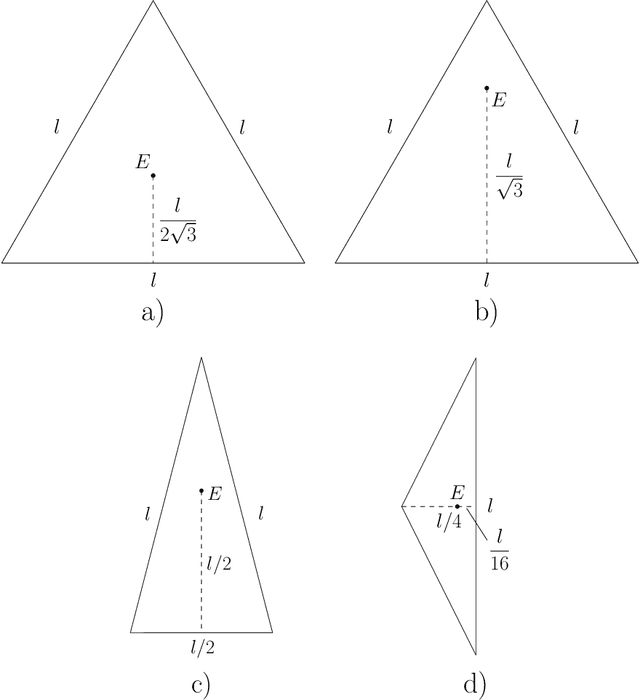
The value of cooperation in pursuit-evasion games is investigated. The considered setting is that of three pursuers chasing one evader in a planar environment. The optimal evader trajectory for a well-known decentralized pursuer strategy is characterized. This result is instrumental to derive upper and lower bounds to the game length, in the case in which the pursuers cooperate in the chasing strategy. It is shown that the cooperation cannot reduce the capture time by more than one half with respect to the decentralized case, and that such bound is tight.

An improved lion strategy for the lion and man problem

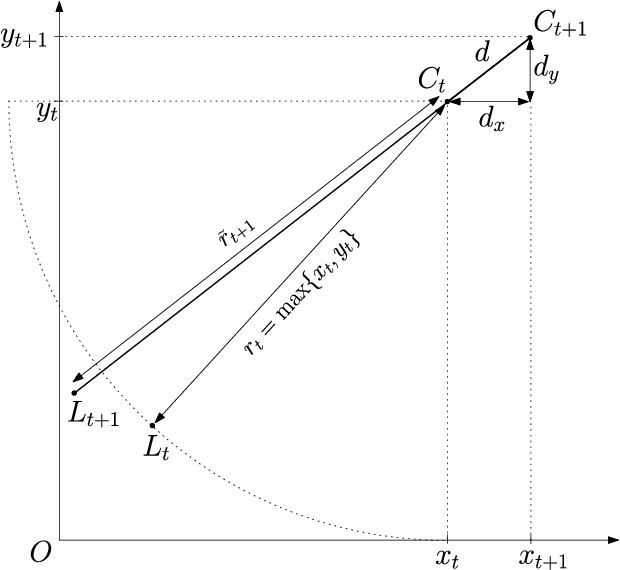
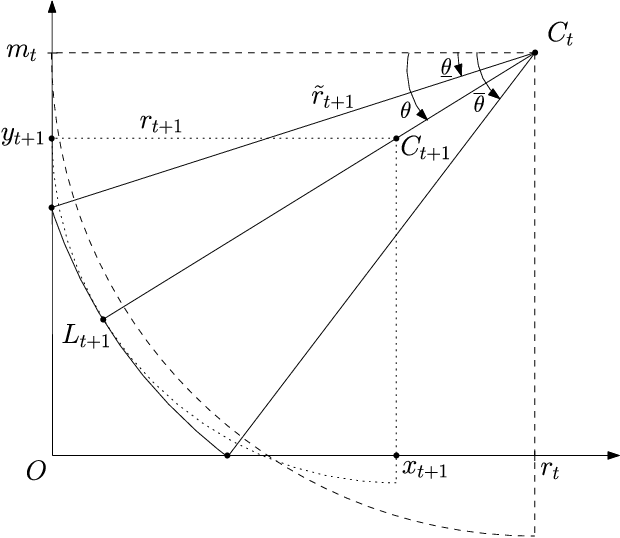
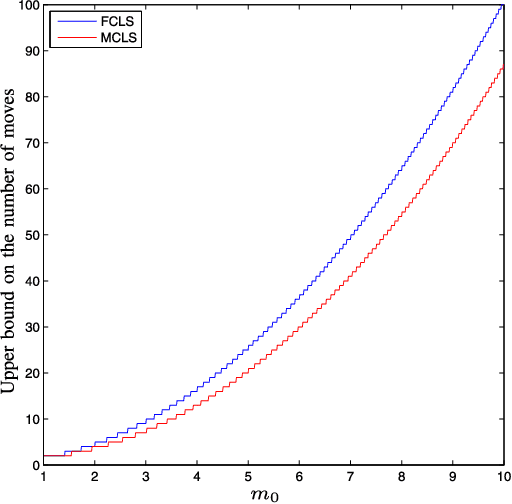
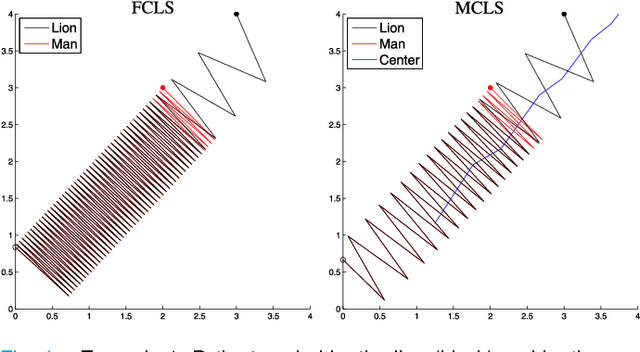
In this paper, a novel lion strategy for David Gale's lion and man problem is proposed. The devised approach enhances a popular strategy proposed by Sgall, which relies on the computation of a suitable "center". The key idea of the new strategy is to update the center at each move, instead of computing it once and for all at the beginning of the game. Convergence of the proposed lion strategy is proven and an upper bound on the game length is derived, which dominates the existing bounds.