An improved lion strategy for the lion and man problem
Paper and Code
Mar 17, 2017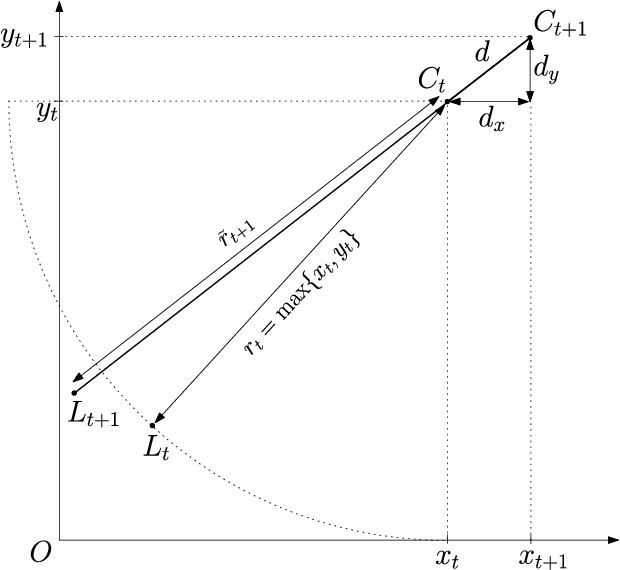
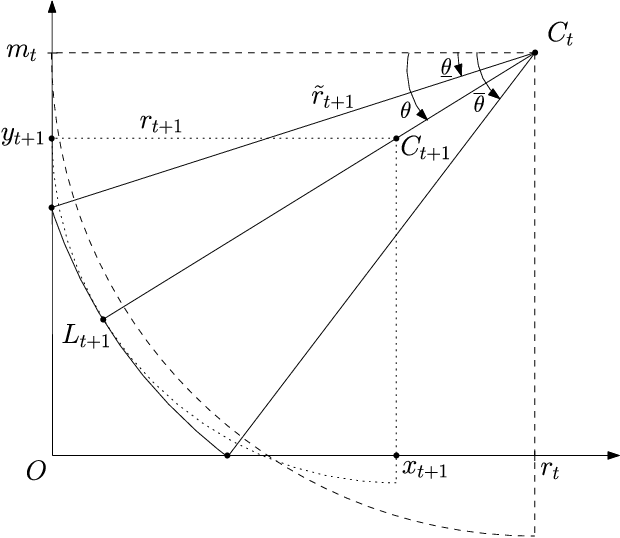
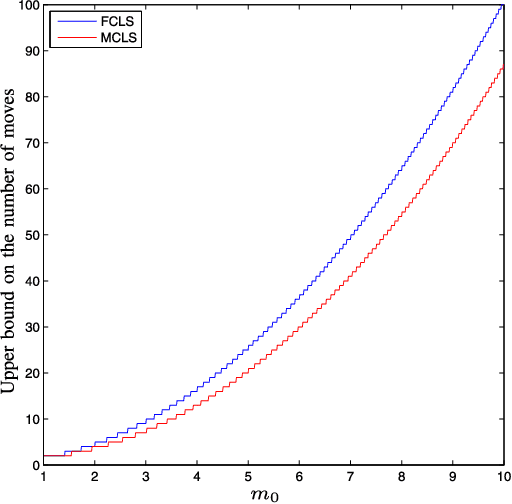
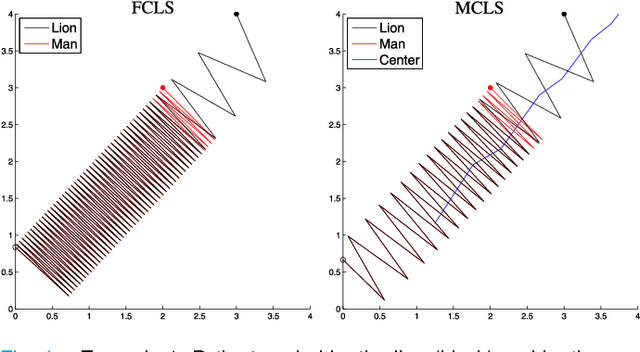
In this paper, a novel lion strategy for David Gale's lion and man problem is proposed. The devised approach enhances a popular strategy proposed by Sgall, which relies on the computation of a suitable "center". The key idea of the new strategy is to update the center at each move, instead of computing it once and for all at the beginning of the game. Convergence of the proposed lion strategy is proven and an upper bound on the game length is derived, which dominates the existing bounds.
* Preprint submitted to IEEE Control Systems Letters
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge