Cybersecurity Detection Classification with Reasoning-enabled Language Models

A major issue in Security Operations Centers (SOCs) is alert fatigue, as the number of detections reported is more than staff can triage in a given day. Prior work prompts or fine-tunes large language models (LLMs) to emit a triage label directly, but does not train them to reason about whether a detection is a genuine threat. We train a chain-of-thought (CoT) reasoning-enabled triage classifier on real, human-labeled Windows endpoint detections by combining automated prompt optimization, self-training, and reinforcement learning with verifiable rewards. We find that CoT reasoning also degrades the label-token probabilities that automated triage relies on, so we separately train a calibrator that reads the full reasoning trace and estimates the probability that the verdict is correct. Our system reaches 82.6% test accuracy and, at the high-confidence operating point that governs automated triage, improves benign recall by 43.0% and malicious recall by 18.3% over a direct-label LLM classifier. We further show that the trained calibrator is necessary - an untrained confidence judge collapses high-confidence recall to zero - and that a finetuned 30B model significantly outperforms frontier general-purpose models, motivating targeted training over scale.

Towards Improved Anomaly Detection for Cloud Cybersecurity via Graph Neural Networks

Detecting security threats in an organization's cloud computing environment has become necessary due to the increased reliance on cloud infrastructure. Logging of all cloud computing events enables investigation into any incidents after they are detected. Automated detection of threats using the logs based on heuristics or anomaly detection could result in a high false positive rate due to its relatively static nature. In this article, we present an industrial case study of a self-supervised learning method using graph neural networks applied to AWS CloudTrail logs to surface suspicious events for analyst review. The model produces an anomaly score for each event and dynamically adapts to changes in the organization without requiring periodic retraining. Based on our experiments across five organizations, the proposed model produced substantially fewer alerts than a domain expert rule-based baseline in almost all cases, reducing alert volumes to approximately 1 per hour from thousands generated by traditional methods. We note that this evaluation covers only flagged events, and false negatives cannot be estimated from the current data; findings should therefore be interpreted as a practical deployment study offering insights into real-world constraints rather than a fully validated detection system. We discuss these limitations and the requirements for extending the approach to other cloud environments as future work.

Fast SVM training using approximate extreme points

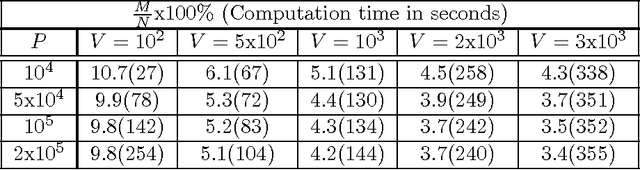
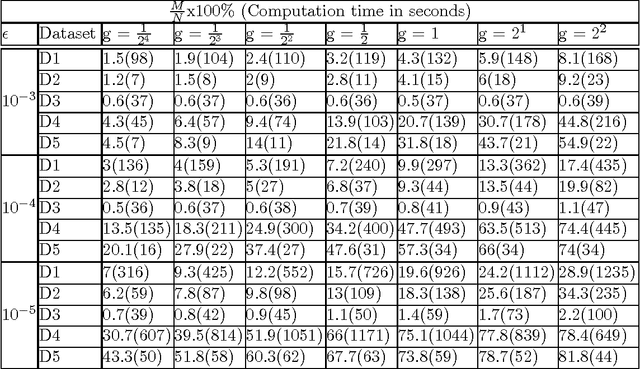
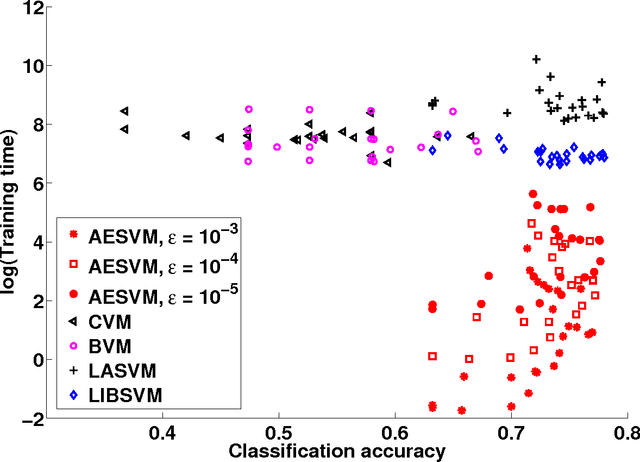
Applications of non-linear kernel Support Vector Machines (SVMs) to large datasets is seriously hampered by its excessive training time. We propose a modification, called the approximate extreme points support vector machine (AESVM), that is aimed at overcoming this burden. Our approach relies on conducting the SVM optimization over a carefully selected subset, called the representative set, of the training dataset. We present analytical results that indicate the similarity of AESVM and SVM solutions. A linear time algorithm based on convex hulls and extreme points is used to compute the representative set in kernel space. Extensive computational experiments on nine datasets compared AESVM to LIBSVM \citep{LIBSVM}, CVM \citep{Tsang05}, BVM \citep{Tsang07}, LASVM \citep{Bordes05}, $\text{SVM}^{\text{perf}}$ \citep{Joachims09}, and the random features method \citep{rahimi07}. Our AESVM implementation was found to train much faster than the other methods, while its classification accuracy was similar to that of LIBSVM in all cases. In particular, for a seizure detection dataset, AESVM training was almost $10^3$ times faster than LIBSVM and LASVM and more than forty times faster than CVM and BVM. Additionally, AESVM also gave competitively fast classification times.