Manabu Kuroki
PCM Selector: Penalized Covariate-Mediator Selection Operator for Evaluating Linear Causal Effects
Dec 24, 2024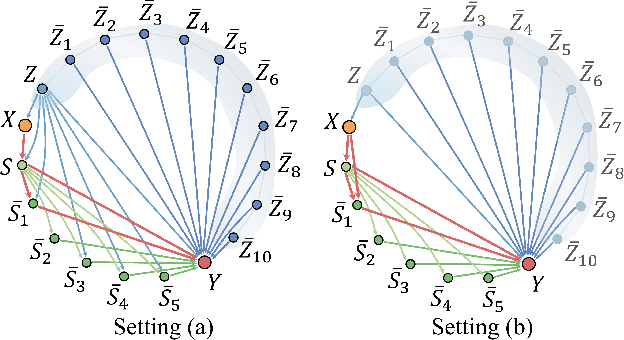
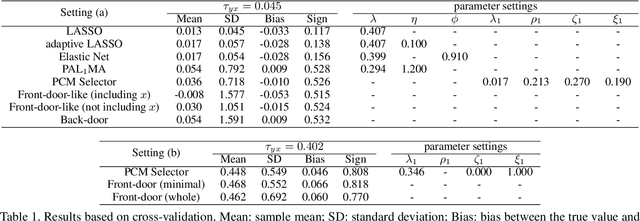
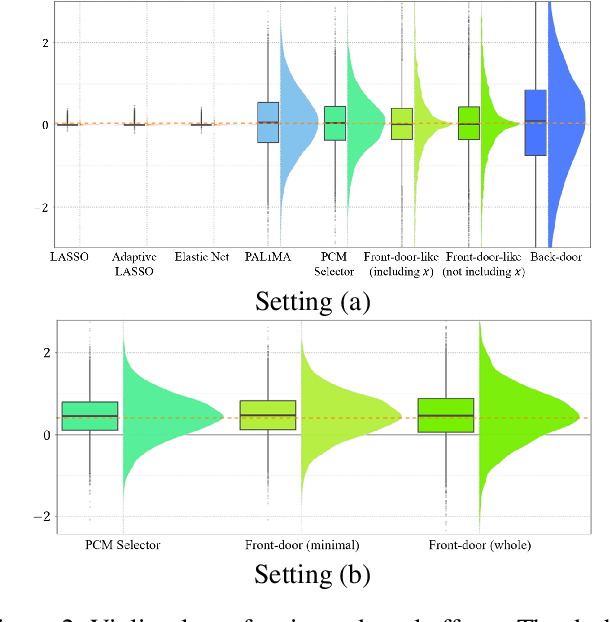
Abstract:For a data-generating process for random variables that can be described with a linear structural equation model, we consider a situation in which (i) a set of covariates satisfying the back-door criterion cannot be observed or (ii) such a set can be observed, but standard statistical estimation methods cannot be applied to estimate causal effects because of multicollinearity/high-dimensional data problems. We propose a novel two-stage penalized regression approach, the penalized covariate-mediator selection operator (PCM Selector), to estimate the causal effects in such scenarios. Unlike existing penalized regression analyses, when a set of intermediate variables is available, PCM Selector provides a consistent or less biased estimator of the causal effect. In addition, PCM Selector provides a variable selection procedure for intermediate variables to obtain better estimation accuracy of the causal effects than does the back-door criterion.
Probabilities of Causation for Continuous and Vector Variables
May 30, 2024Abstract:Probabilities of causation (PoC) are valuable concepts for explainable artificial intelligence and practical decision-making. PoC are originally defined for scalar binary variables. In this paper, we extend the concept of PoC to continuous treatment and outcome variables, and further generalize PoC to capture causal effects between multiple treatments and multiple outcomes. In addition, we consider PoC for a sub-population and PoC with multi-hypothetical terms to capture more sophisticated counterfactual information useful for decision-making. We provide a nonparametric identification theorem for each type of PoC we introduce. Finally, we illustrate the application of our results on a real-world dataset about education.
Identification and Estimation of Conditional Average Partial Causal Effects via Instrumental Variable
Jan 20, 2024Abstract:There has been considerable recent interest in estimating heterogeneous causal effects. In this paper, we introduce conditional average partial causal effects (CAPCE) to reveal the heterogeneity of causal effects with continuous treatment. We provide conditions for identifying CAPCE in an instrumental variable setting. We develop three families of CAPCE estimators: sieve, parametric, and reproducing kernel Hilbert space (RKHS)-based, and analyze their statistical properties. We illustrate the proposed CAPCE estimators on synthetic and real-world data.
Selection of Identifiability Criteria for Total Effects by using Path Diagrams
Jul 11, 2012Abstract:Pearl has provided the back door criterion, the front door criterion and the conditional instrumental variable (IV) method as identifiability criteria for total effects. In some situations, these three criteria can be applied to identifying total effects simultaneously. For the purpose of increasing estimating accuracy, this paper compares the three ways of identifying total effects in terms of the asymptotic variance, and concludes that in some situations the superior of them can be recognized directly from the graph structure.
The Graphical Identification for Total Effects by using Surrogate Variables
Jul 04, 2012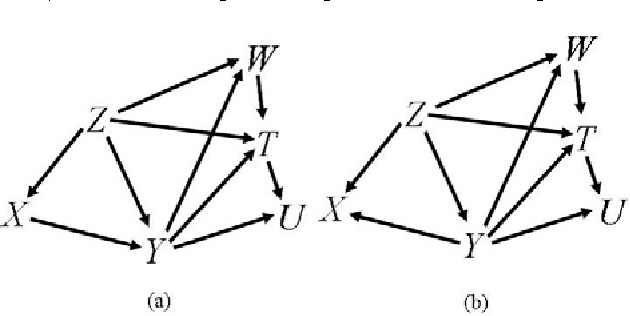
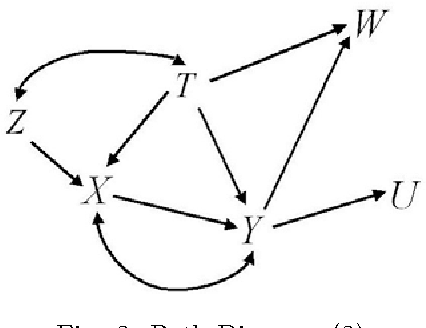
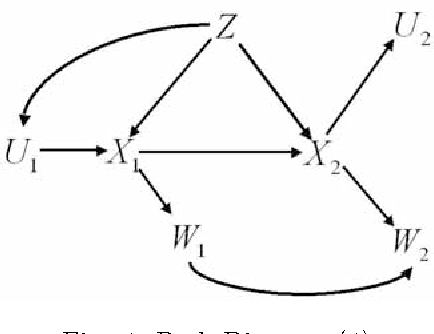
Abstract:Consider the case where cause-effect relationships between variables can be described as a directed acyclic graph and the corresponding linear structural equation model. This paper provides graphical identifiability criteria for total effects by using surrogate variables in the case where it is difficult to observe a treatment/response variable. The results enable us to judge from graph structure whether a total effect can be identified through the observation of surrogate variables.
Counterfactual Reasoning in Linear Structural Equation Models
Jul 04, 2012Abstract:Consider the case where causal relations among variables can be described as a Gaussian linear structural equation model. This paper deals with the problem of clarifying how the variance of a response variable would have changed if a treatment variable were assigned to some value (counterfactually), given that a set of variables is observed (actually). In order to achieve this aim, we reformulate the formulas of the counterfactual distribution proposed by Balke and Pearl (1995) through both the total effects and a covariance matrix of observed variables. We further extend the framework of Balke and Pearl (1995) from point observations to interval observations, and from an unconditional plan to a conditional plan. The results of this paper enable us to clarify the properties of counterfactual distribution and establish an optimal plan.
Stratified Analysis of `Probabilities of Causation'
Jun 27, 2012
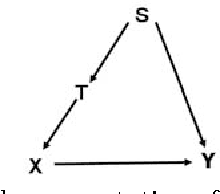
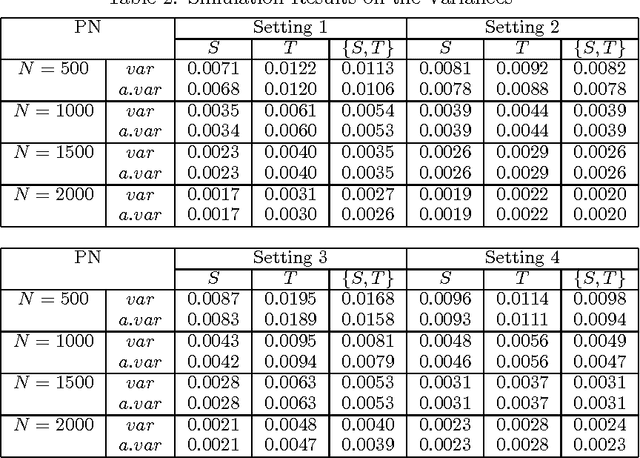
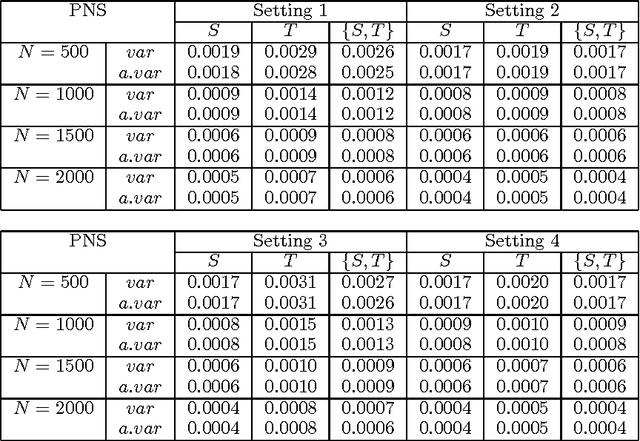
Abstract:This paper proposes new formulas for the probabilities of causation difined by Pearl (2000). Tian and Pearl (2000a, 2000b) showed how to bound the quantities of the probabilities of causation from experimental and observational data, under the minimal assumptions about the data-generating process. We derive narrower bounds than Tian-Pearl bounds by making use of the covariate information measured in experimental and observational studies. In addition, we provide identifiable case under no-prevention assumption and discuss the covariate selection problem from the viewpoint of estimation accuracy. These results are helpful in providing more evidence for public policy assessment and dicision making problems.
Evaluation of the Causal Effect of Control Plans in Nonrecursive Structural Equation Models
Jun 20, 2012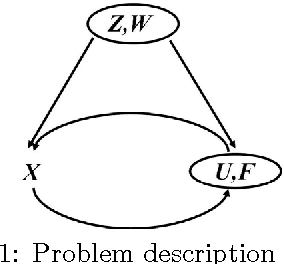
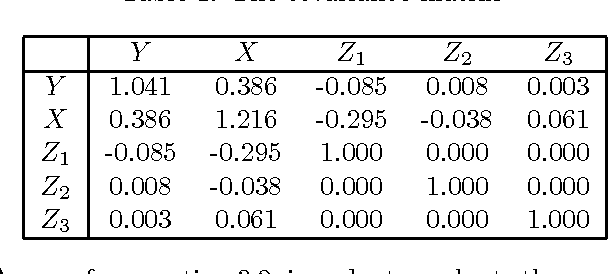
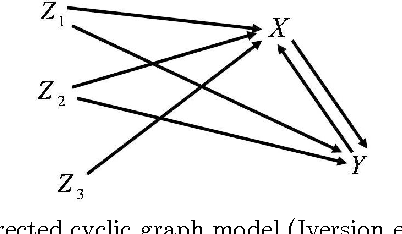
Abstract:When observational data is available from practical studies and a directed cyclic graph for how various variables affect each other is known based on substantive understanding of the process, we consider a problem in which a control plan of a treatment variable is conducted in order to bring a response variable close to a target value with variation reduction. We formulate an optimal control plan concerning a certain treatment variable through path coefficients in the framework of linear nonrecursive structural equation models. Based on the formulation, we clarify the properties of causal effects when conducting a control plan. The results enable us to evaluate the effect of a control plan on the variance from observational data.
The Evaluation of Causal Effects in Studies with an Unobserved Exposure/Outcome Variable: Bounds and Identification
Jun 13, 2012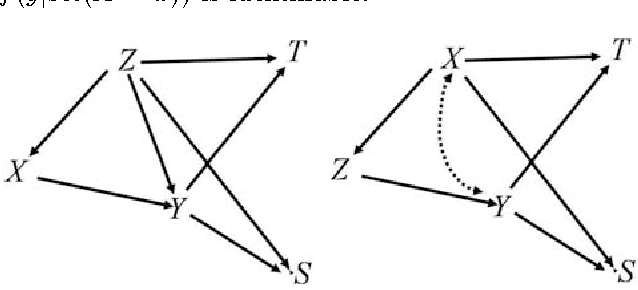
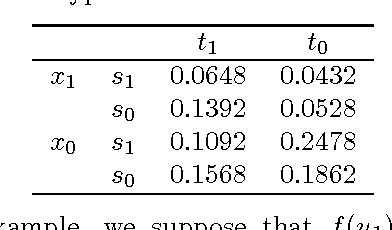
Abstract:This paper deals with the problem of evaluating the causal effect using observational data in the presence of an unobserved exposure/ outcome variable, when cause-effect relationships between variables can be described as a directed acyclic graph and the corresponding recursive factorization of a joint distribution. First, we propose identifiability criteria for causal effects when an unobserved exposure/outcome variable is considered to contain more than two categories. Next, when unmeasured variables exist between an unobserved outcome variable and its proxy variables, we provide the tightest bounds based on the potential outcome approach. The results of this paper are helpful to evaluate causal effects in the case where it is difficult or expensive to observe an exposure/ outcome variable in many practical fields.
On Identifying Total Effects in the Presence of Latent Variables and Selection bias
Jun 13, 2012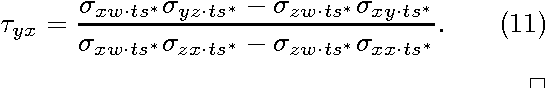
Abstract:Assume that cause-effect relationships between variables can be described as a directed acyclic graph and the corresponding linear structural equation model.We consider the identification problem of total effects in the presence of latent variables and selection bias between a treatment variable and a response variable. Pearl and his colleagues provided the back door criterion, the front door criterion (Pearl, 2000) and the conditional instrumental variable method (Brito and Pearl, 2002) as identifiability criteria for total effects in the presence of latent variables, but not in the presence of selection bias. In order to solve this problem, we propose new graphical identifiability criteria for total effects based on the identifiable factor models. The results of this paper are useful to identify total effects in observational studies and provide a new viewpoint to the identification conditions of factor models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge