Joint Linked Component Analysis for Multiview Data

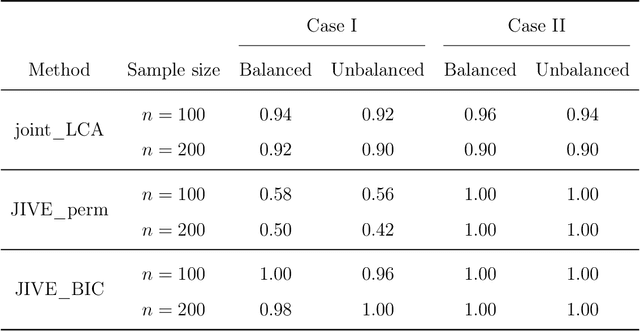
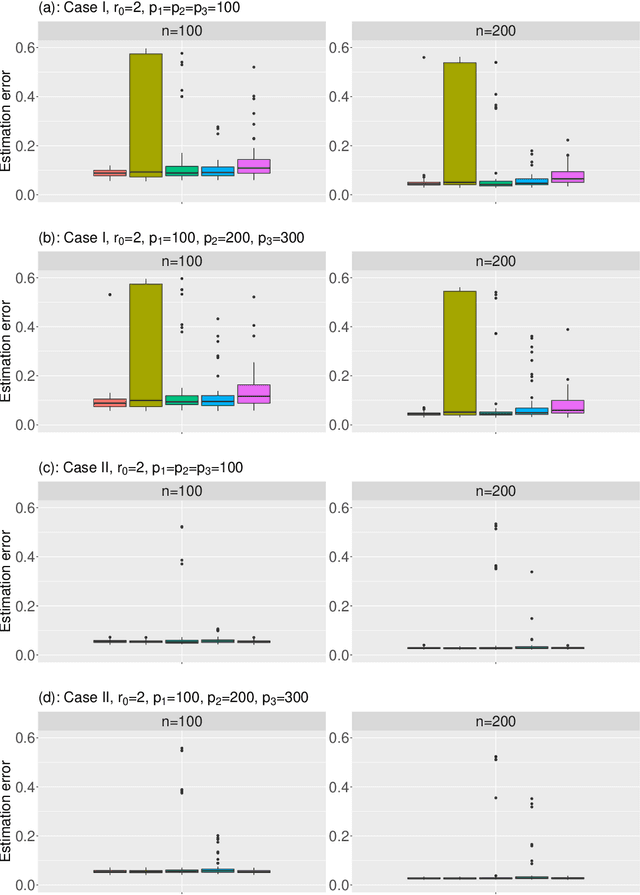
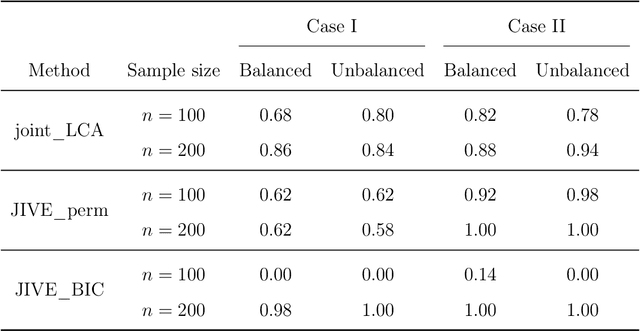
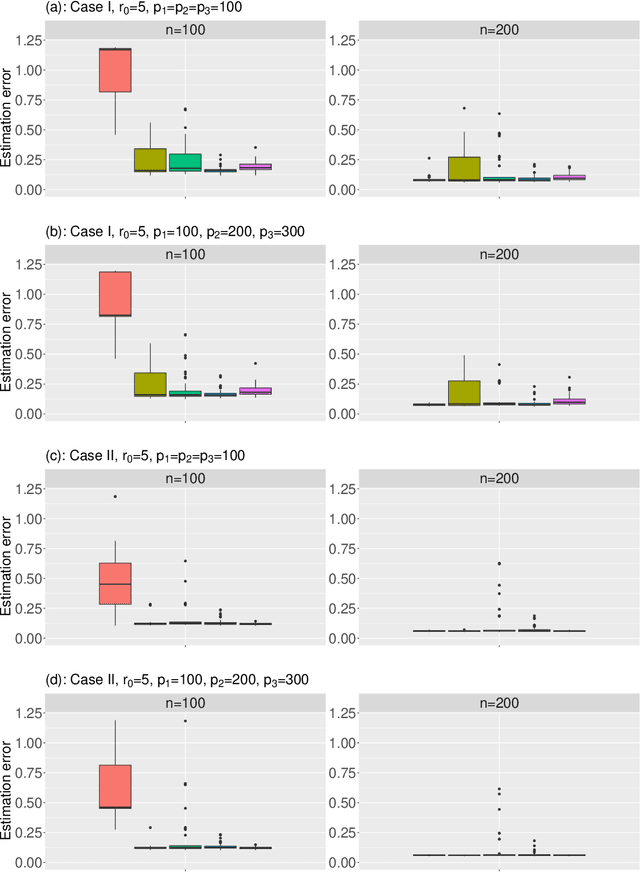
In this work, we propose the joint linked component analysis (joint\_LCA) for multiview data. Unlike classic methods which extract the shared components in a sequential manner, the objective of joint\_LCA is to identify the view-specific loading matrices and the rank of the common latent subspace simultaneously. We formulate a matrix decomposition model where a joint structure and an individual structure are present in each data view, which enables us to arrive at a clean svd representation for the cross covariance between any pair of data views. An objective function with a novel penalty term is then proposed to achieve simultaneous estimation and rank selection. In addition, a refitting procedure is employed as a remedy to reduce the shrinkage bias caused by the penalization.

Convex Banding of the Covariance Matrix

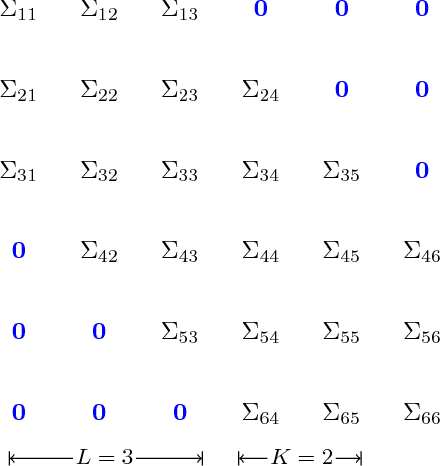
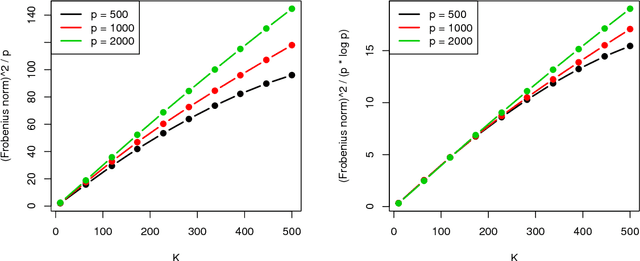
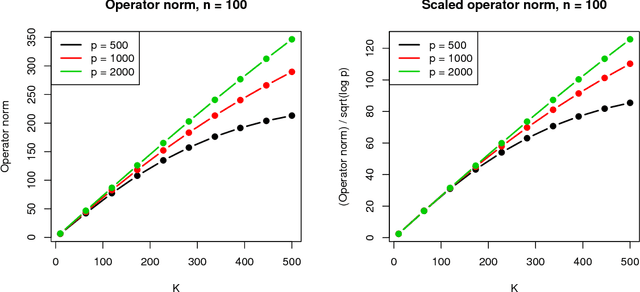
We introduce a new sparse estimator of the covariance matrix for high-dimensional models in which the variables have a known ordering. Our estimator, which is the solution to a convex optimization problem, is equivalently expressed as an estimator which tapers the sample covariance matrix by a Toeplitz, sparsely-banded, data-adaptive matrix. As a result of this adaptivity, the convex banding estimator enjoys theoretical optimality properties not attained by previous banding or tapered estimators. In particular, our convex banding estimator is minimax rate adaptive in Frobenius and operator norms, up to log factors, over commonly-studied classes of covariance matrices, and over more general classes. Furthermore, it correctly recovers the bandwidth when the true covariance is exactly banded. Our convex formulation admits a simple and efficient algorithm. Empirical studies demonstrate its practical effectiveness and illustrate that our exactly-banded estimator works well even when the true covariance matrix is only close to a banded matrix, confirming our theoretical results. Our method compares favorably with all existing methods, in terms of accuracy and speed. We illustrate the practical merits of the convex banding estimator by showing that it can be used to improve the performance of discriminant analysis for classifying sound recordings.