Gauge-optimal approximate learning for small data classification problems

Small data learning problems are characterized by a significant discrepancy between the limited amount of response variable observations and the large feature space dimension. In this setting, the common learning tools struggle to identify the features important for the classification task from those that bear no relevant information, and cannot derive an appropriate learning rule which allows to discriminate between different classes. As a potential solution to this problem, here we exploit the idea of reducing and rotating the feature space in a lower-dimensional gauge and propose the Gauge-Optimal Approximate Learning (GOAL) algorithm, which provides an analytically tractable joint solution to the dimension reduction, feature segmentation and classification problems for small data learning problems. We prove that the optimal solution of the GOAL algorithm consists in piecewise-linear functions in the Euclidean space, and that it can be approximated through a monotonically convergent algorithm which presents -- under the assumption of a discrete segmentation of the feature space -- a closed-form solution for each optimization substep and an overall linear iteration cost scaling. The GOAL algorithm has been compared to other state-of-the-art machine learning (ML) tools on both synthetic data and challenging real-world applications from climate science and bioinformatics (i.e., prediction of the El Nino Southern Oscillation and inference of epigenetically-induced gene-activity networks from limited experimental data). The experimental results show that the proposed algorithm outperforms the reported best competitors for these problems both in learning performance and computational cost.

Linearly-scalable learning of smooth low-dimensional patterns with permutation-aided entropic dimension reduction

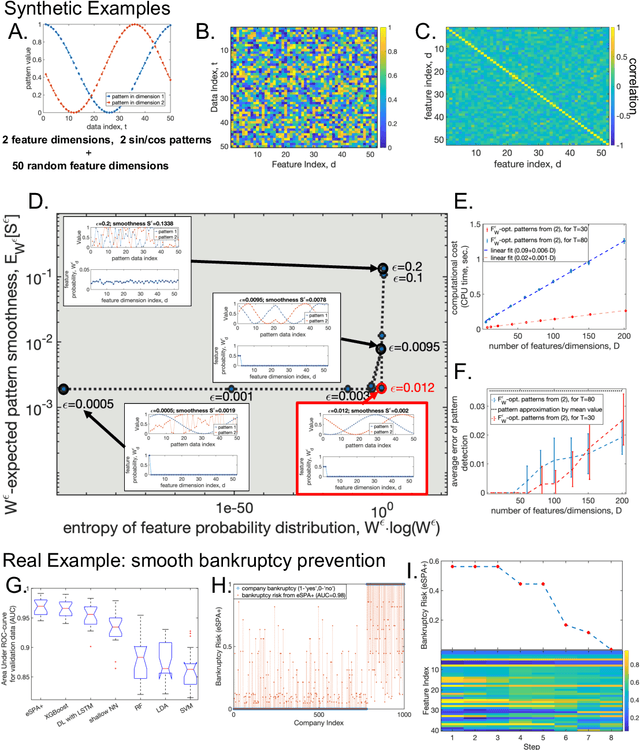
In many data science applications, the objective is to extract appropriately-ordered smooth low-dimensional data patterns from high-dimensional data sets. This is challenging since common sorting algorithms are primarily aiming at finding monotonic orderings in low-dimensional data, whereas typical dimension reduction and feature extraction algorithms are not primarily designed for extracting smooth low-dimensional data patterns. We show that when selecting the Euclidean smoothness as a pattern quality criterium, both of these problems (finding the optimal 'crisp' data permutation and extracting the sparse set of permuted low-dimensional smooth patterns) can be efficiently solved numerically as one unsupervised entropy-regularized iterative optimization problem. We formulate and prove the conditions for monotonicity and convergence of this linearly-scalable (in dimension) numerical procedure, with the iteration cost scaling of $\mathcal{O}(DT^2)$, where $T$ is the size of the data statistics and $D$ is a feature space dimension. The efficacy of the proposed method is demonstrated through the examination of synthetic examples as well as a real-world application involving the identification of smooth bankruptcy risk minimizing transition patterns from high-dimensional economical data. The results showcase that the statistical properties of the overall time complexity of the method exhibit linear scaling in the dimensionality $D$ within the specified confidence intervals.