Lukas Polok
Highly Efficient Compact Pose SLAM with SLAM++
Aug 10, 2016
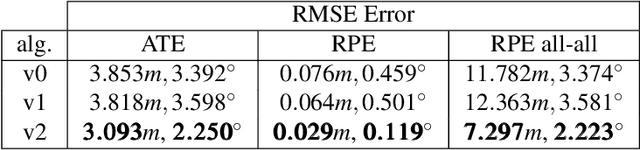
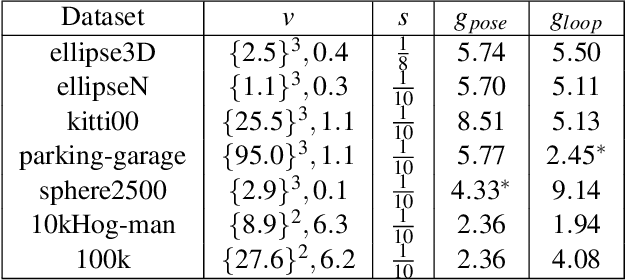
Abstract:Maximum likelihood estimation (MLE) is a well-known estimation method used in many robotic and computer vision applications. Under Gaussian assumption, the MLE converts to a nonlinear least squares (NLS) problem. Efficient solutions to NLS exist and they are based on iteratively solving sparse linear systems until convergence. In general, the existing solutions provide only an estimation of the mean state vector, the resulting covariance being computationally too expensive to recover. Nevertheless, in many simultaneous localisation and mapping (SLAM) applications, knowing only the mean vector is not enough. Data association, obtaining reduced state representations, active decisions and next best view are only a few of the applications that require fast state covariance recovery. Furthermore, computer vision and robotic applications are in general performed online. In this case, the state is updated and recomputed every step and its size is continuously growing, therefore, the estimation process may become highly computationally demanding. This paper introduces a general framework for incremental MLE called SLAM++, which fully benefits from the incremental nature of the online applications, and provides efficient estimation of both the mean and the covariance of the estimate. Based on that, we propose a strategy for maintaining a sparse and scalable state representation for large scale mapping, which uses information theory measures to integrate only informative and non-redundant contributions to the state representation. SLAM++ differs from existing implementations by performing all the matrix operations by blocks. This led to extremely fast matrix manipulation and arithmetic operations. Even though this paper tests SLAM++ efficiency on SLAM problems, its applicability remains general.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge