Least Squares Training of Quadratic Convolutional Neural Networks with Applications to System Theory

This paper provides a least squares formulation for the training of a 2-layer convolutional neural network using quadratic activation functions, a 2-norm loss function, and no regularization term. Using this method, an analytic expression for the globally optimal weights is obtained alongside a quadratic input-output equation for the network. These properties make the network a viable tool in system theory by enabling further analysis, such as the sensitivity of the output to perturbations in the input, which is crucial for safety-critical systems such as aircraft or autonomous vehicles.The least squares method is compared to previously proposed strategies for training quadratic networks and to a back-propagation-trained ReLU network. The proposed method is applied to a system identification problem and a GPS position estimation problem. The least squares network is shown to have a significantly reduced training time with minimal compromises on prediction accuracy alongside the advantages of having an analytic input-output equation. Although these results only apply to 2-layer networks, this paper motivates the exploration of deeper quadratic networks in the context of system theory.

Analysis and Design of Quadratic Neural Networks for Regression, Classification, and Lyapunov Control of Dynamical Systems

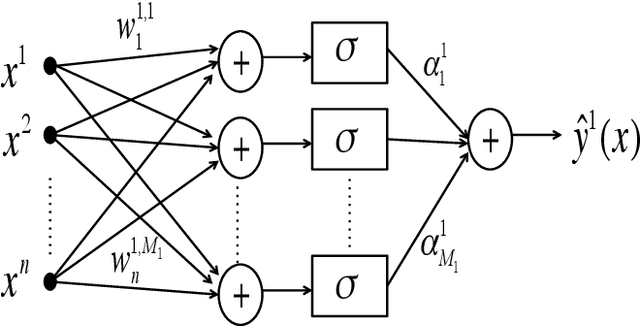
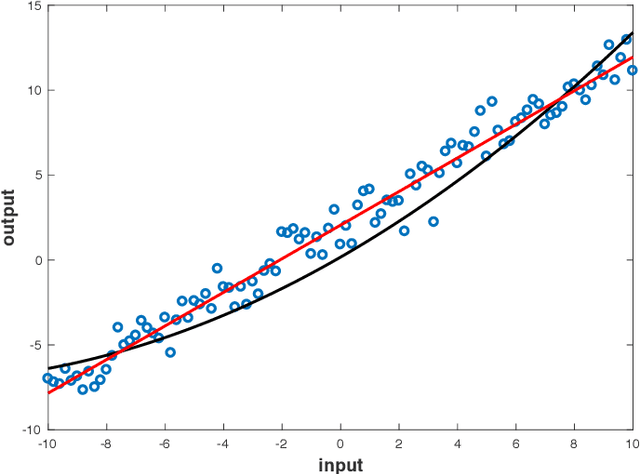
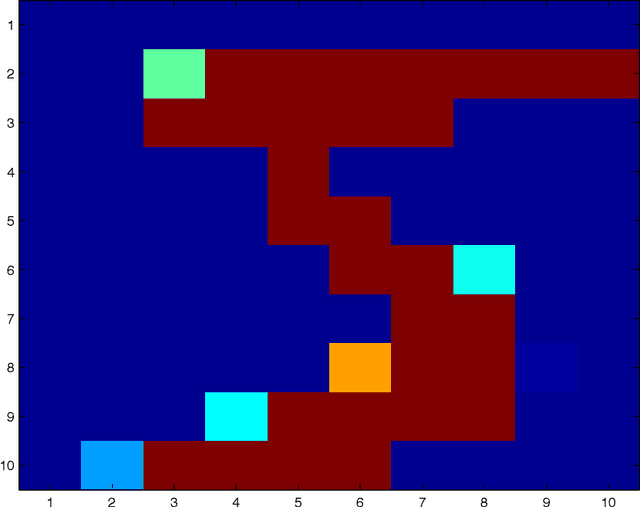
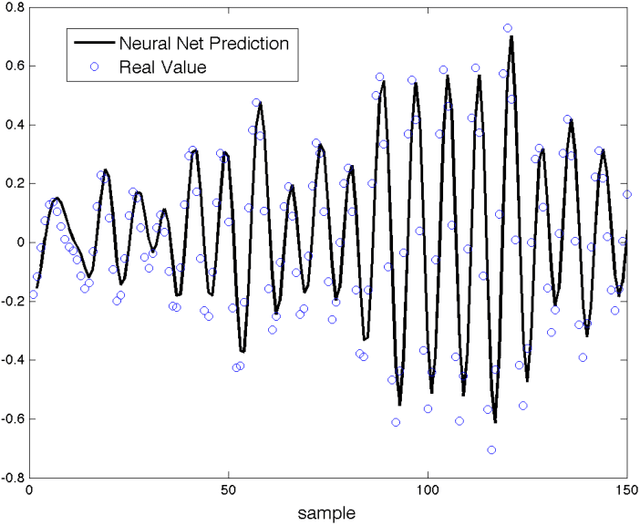
This paper addresses the analysis and design of quadratic neural networks, which have been recently introduced in the literature, and their applications to regression, classification, system identification and control of dynamical systems. These networks offer several advantages, the most important of which are the fact that the architecture is a by-product of the design and is not determined a-priori, their training can be done by solving a convex optimization problem so that the global optimum of the weights is achieved, and the input-output mapping can be expressed analytically by a quadratic form. It also appears from several examples that these networks work extremely well using only a small fraction of the training data. The results in the paper cast regression, classification, system identification, stability and control design as convex optimization problems, which can be solved efficiently with polynomial-time algorithms to a global optimum. Several examples will show the effectiveness of quadratic neural networks in applications.