Abstract argumentation and answer set programming: two faces of Nelson's logic

In this work, we show that both logic programming and abstract argumentation frameworks can be interpreted in terms of Nelson's constructive logic N4. We do so by formalizing, in this logic, two principles that we call non-contradictory inference and strengthened closed world assumption: the first states that no belief can be held based on contradictory evidence while the latter forces both unknown and contradictory evidence to be regarded as false. Using these principles, both logic programming and abstract argumentation frameworks are translated into constructive logic in a modular way and using the object language. Logic programming implication and abstract argumentation supports become, in the translation, a new implication connective following the non-contradictory inference principle. Attacks are then represented by combining this new implication with strong negation. Under consideration in Theory and Practice of Logic Programming (TPLP).

Dynamic Epistemic Logic with ASP Updates: Application to Conditional Planning

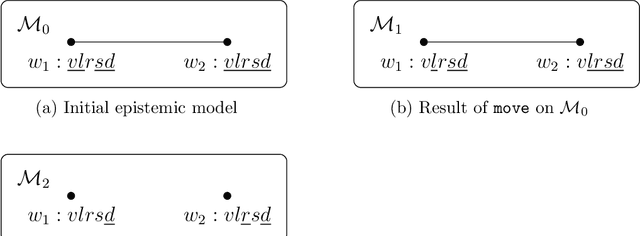
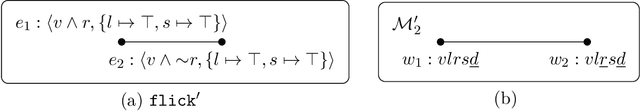
Dynamic Epistemic Logic (DEL) is a family of multimodal logics that has proved to be very successful for epistemic reasoning in planning tasks. In this logic, the agent's knowledge is captured by modal epistemic operators whereas the system evolution is described in terms of (some subset of) dynamic logic modalities in which actions are usually represented as semantic objects called event models. In this paper, we study a variant of DEL, that wecall DEL[ASP], where actions are syntactically described by using an Answer Set Programming (ASP) representation instead of event models. This representation directly inherits high level expressive features like indirect effects, qualifications, state constraints, defaults, or recursive fluents that are common in ASP descriptions of action domains. Besides, we illustrate how this approach can be applied for obtaining conditional plans in single-agent, partially observable domains where knowledge acquisition may be represented as indirect effects of actions.

Splitting Epistemic Logic Programs

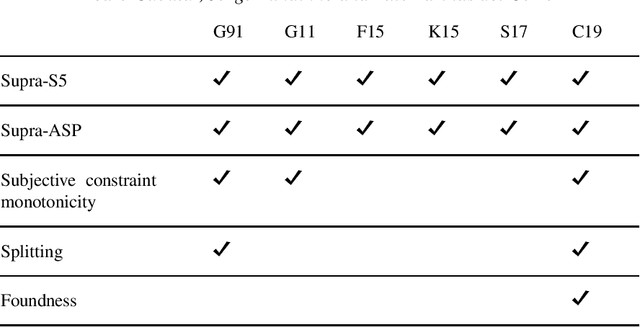
Epistemic logic programs constitute an extension of the stable models semantics to deal with new constructs called subjective literals. Informally speaking, a subjective literal allows checking whether some regular literal is true in all stable models or in some stable model. As it can be imagined, the associated semantics has proved to be non-trivial, as the truth of the subjective literal may interfere with the set of stable models it is supposed to query. As a consequence, no clear agreement has been reached and different semantic proposals have been made in the literature. Unfortunately, comparison among these proposals has been limited to a study of their effect on individual examples, rather than identifying general properties to be checked. In this paper, we propose an extension of the well-known splitting property for logic programs to the epistemic case. To this aim, we formally define when an arbitrary semantics satisfies the epistemic splitting property and examine some of the consequences that can be derived from that, including its relation to conformant planning and to epistemic constraints. Interestingly, we prove (through counterexamples) that most of the existing proposals fail to fulfill the epistemic splitting property, except the original semantics proposed by Gelfond in 1991.

Functional ASP with Intensional Sets: Application to Gelfond-Zhang Aggregates

In this paper, we propose a variant of Answer Set Programming (ASP) with evaluable functions that extends their application to sets of objects, something that allows a fully logical treatment of aggregates. Formally, we start from the syntax of First Order Logic with equality and the semantics of Quantified Equilibrium Logic with evaluable functions (QELF). Then, we proceed to incorporate a new kind of logical term, intensional set (a construct commonly used to denote the set of objects characterised by a given formula), and to extend QELF semantics for this new type of expression. In our extended approach, intensional sets can be arbitrarily used as predicate or function arguments or even nested inside other intensional sets, just as regular first-order logical terms. As a result, aggregates can be naturally formed by the application of some evaluable function (count, sum, maximum, etc) to a set of objects expressed as an intensional set. This approach has several advantages. First, while other semantics for aggregates depend on some syntactic transformation (either via a reduct or a formula translation), the QELF interpretation treats them as regular evaluable functions, providing a compositional semantics and avoiding any kind of syntactic restriction. Second, aggregates can be explicitly defined now within the logical language by the simple addition of formulas that fix their meaning in terms of multiple applications of some (commutative and associative) binary operation. For instance, we can use recursive rules to define sum in terms of integer addition. Last, but not least, we prove that the semantics we obtain for aggregates coincides with the one defined by Gelfond and Zhang for the Alog language, when we restrict to that syntactic fragment. (Under consideration for acceptance in TPLP)