The Best Path Algorithm automatic variables selection via High Dimensional Graphical Models

This paper proposes a new algorithm for an automatic variable selection procedure in High Dimensional Graphical Models. The algorithm selects the relevant variables for the node of interest on the basis of mutual information. Several contributions in literature have investigated the use of mutual information in selecting the appropriate number of relevant features in a large data-set, but most of them have focused on binary outcomes or required high computational effort. The algorithm here proposed overcomes these drawbacks as it is an extension of Chow and Liu's algorithm. Once, the probabilistic structure of a High Dimensional Graphical Model is determined via the said algorithm, the best path-step, including variables with the most explanatory/predictive power for a variable of interest, is determined via the computation of the entropy coefficient of determination. The latter, being based on the notion of (symmetric) Kullback-Leibler divergence, turns out to be closely connected to the mutual information of the involved variables. The application of the algorithm to a wide range of real-word and publicly data-sets has highlighted its potential and greater effectiveness compared to alternative extant methods.

Use of High Dimensional Modeling for automatic variables selection: the best path algorithm

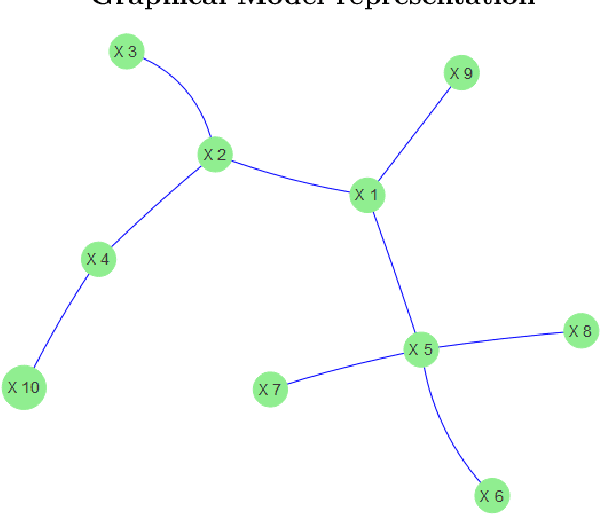
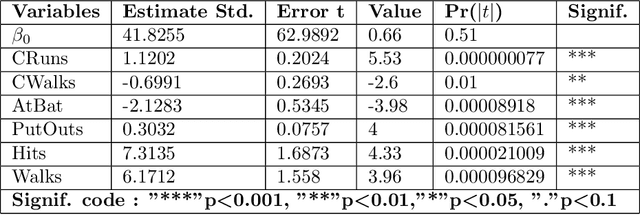
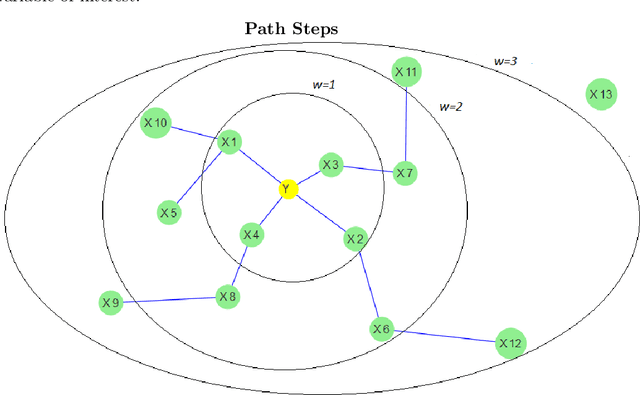
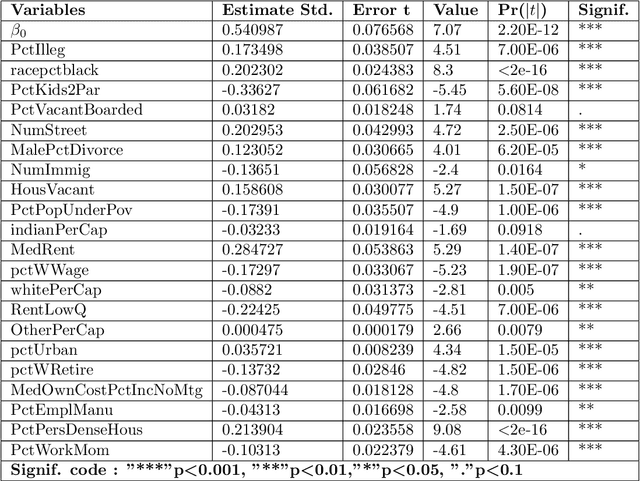
This paper presents a new algorithm for automatic variables selection. In particular, using the Graphical Models properties it is possible to develop a method that can be used in the contest of large dataset. The advantage of this algorithm is that can be combined with different forecasting models. In this research we have used the OLS method and we have compared the result with the LASSO method.

Drift Estimation with Graphical Models

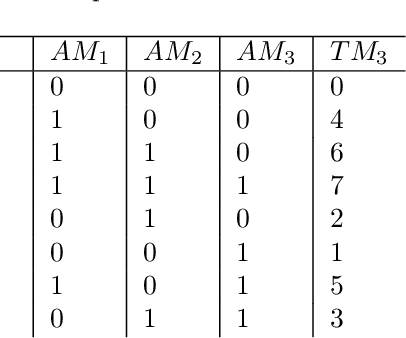
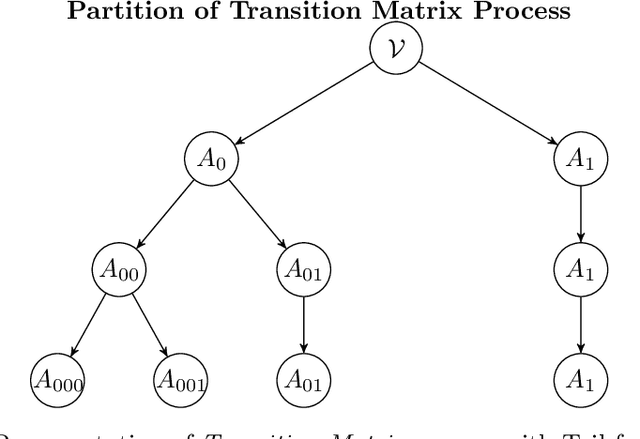
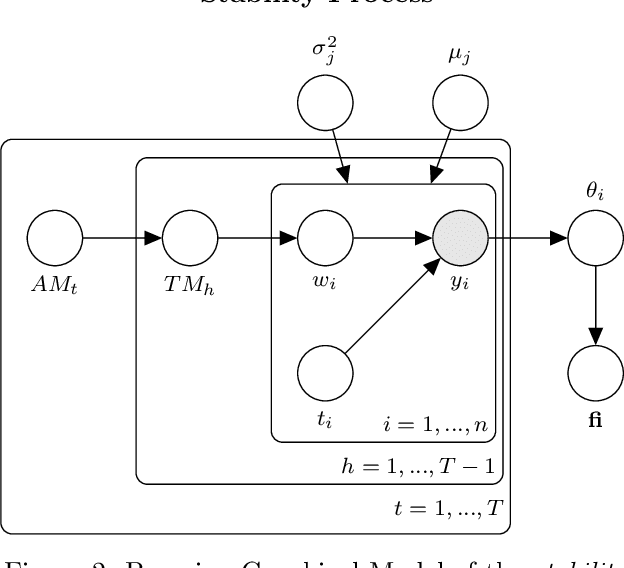
This paper deals with the issue of concept drift in supervised machine learn-ing. We make use of graphical models to elicit the visible structure of the dataand we infer from there changes in the hidden context. Differently from previous concept-drift detection methods, this application does not depend on the supervised machine learning model in use for a specific target variable, but it tries to assess the concept drift as independent characteristic of the evolution of a dataset. Specifically, we investigate how a graphical model evolves by looking at the creation of new links and the disappearing of existing ones in different time periods. The paper suggests a method that highlights the changes and eventually produce a metric to evaluate the stability over time. The paper evaluate the method with real world data on the Australian Electric market.