The Best Path Algorithm automatic variables selection via High Dimensional Graphical Models

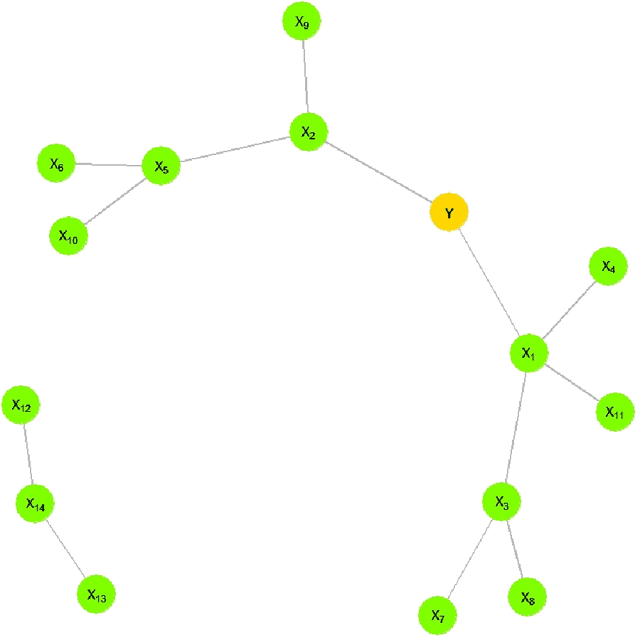
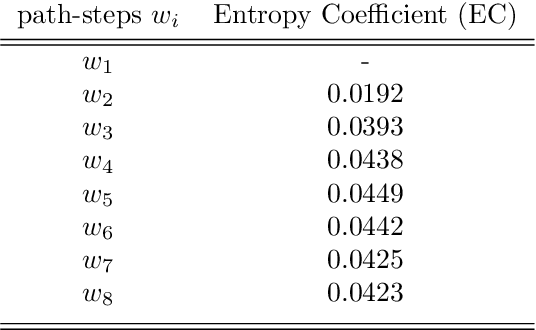
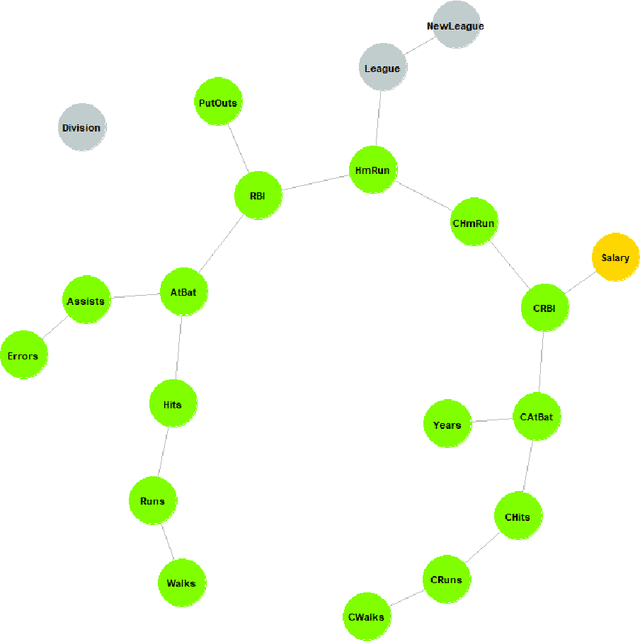
This paper proposes a new algorithm for an automatic variable selection procedure in High Dimensional Graphical Models. The algorithm selects the relevant variables for the node of interest on the basis of mutual information. Several contributions in literature have investigated the use of mutual information in selecting the appropriate number of relevant features in a large data-set, but most of them have focused on binary outcomes or required high computational effort. The algorithm here proposed overcomes these drawbacks as it is an extension of Chow and Liu's algorithm. Once, the probabilistic structure of a High Dimensional Graphical Model is determined via the said algorithm, the best path-step, including variables with the most explanatory/predictive power for a variable of interest, is determined via the computation of the entropy coefficient of determination. The latter, being based on the notion of (symmetric) Kullback-Leibler divergence, turns out to be closely connected to the mutual information of the involved variables. The application of the algorithm to a wide range of real-word and publicly data-sets has highlighted its potential and greater effectiveness compared to alternative extant methods.