EISPY2D: An Open-Source Python Library for the Development and Comparison of Algorithms in Two-Dimensional Electromagnetic Inverse Scattering Problems

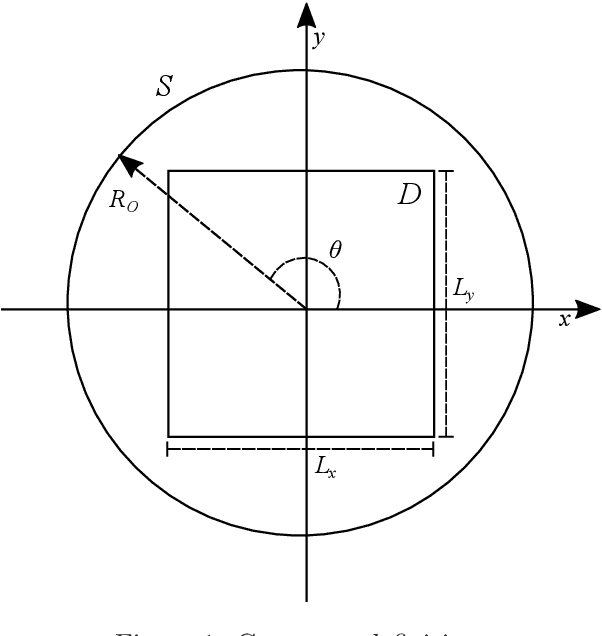
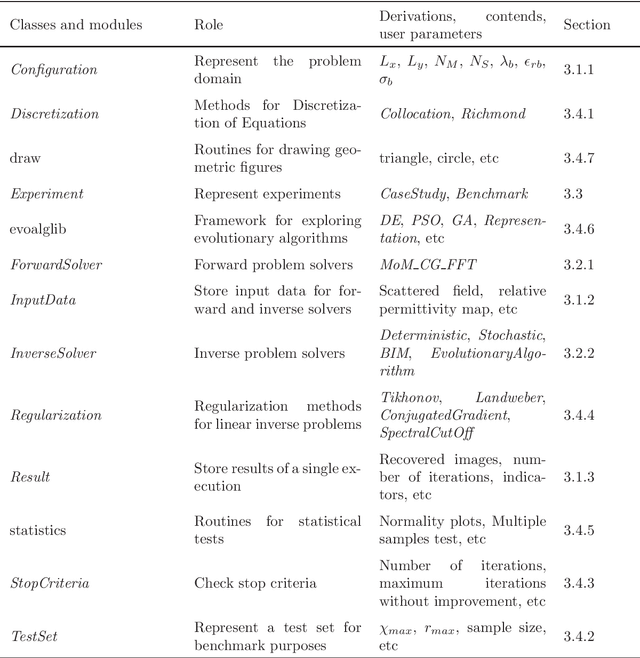
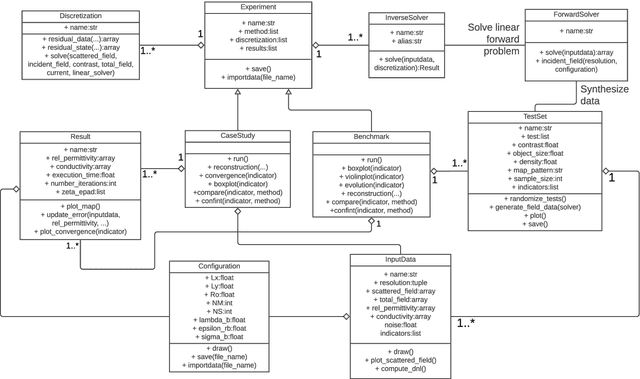
Microwave Imaging is an essential technique for reconstructing the electrical properties of an inaccessible medium. Many approaches have been proposed employing algorithms to solve the Electromagnetic Inverse Scattering Problem associated with this technique. In addition to the algorithm, one needs to implement adequate structures to represent the problem domain, the input data, the results of the adopted metrics, and experimentation routines. We introduce an open-source Python library that offers a modular and standardized framework for implementing and evaluating the performance of algorithms for the problem. Based on the implementation of fundamental components for the execution of algorithms, this library aims to facilitate the development and discussion of new methods. Through a modular structure organized into classes, researchers can design their case studies and benchmarking experiments relying on features such as test randomization, specific metrics, and statistical comparison. To the best of the authors' knowledge, it is the first time that such tools for benchmarking and comparison are introduced for microwave imaging algorithms. In addition, two new metrics for location and shape recovery are presented. In this work, we introduce the principles for the design of the problem components and provide studies to exemplify the main aspects of this library. It is freely distributed through a Github repository that can be accessed from https://andre-batista.github.io/eispy2d/.

The Cone epsilon-Dominance: An Approach for Evolutionary Multiobjective Optimization

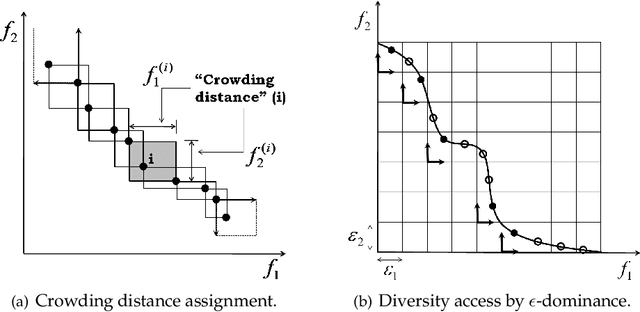
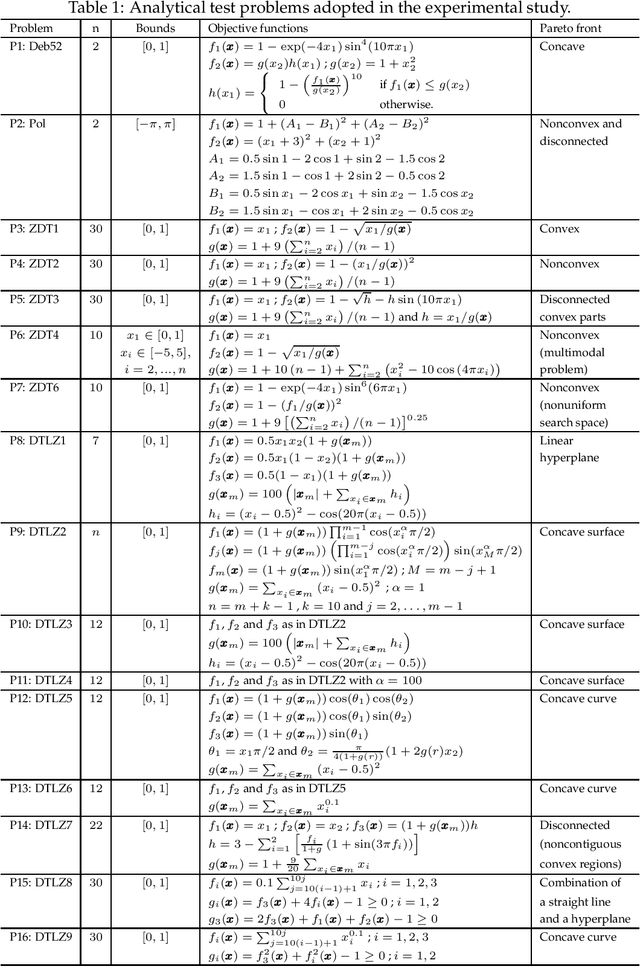
We propose the cone epsilon-dominance approach to improve convergence and diversity in multiobjective evolutionary algorithms (MOEAs). A cone-eps-MOEA is presented and compared with MOEAs based on the standard Pareto relation (NSGA-II, NSGA-II*, SPEA2, and a clustered NSGA-II) and on the epsilon-dominance (eps-MOEA). The comparison is performed both in terms of computational complexity and on four performance indicators selected to quantify the quality of the final results obtained by each algorithm: the convergence, diversity, hypervolume, and coverage of many sets metrics. Sixteen well-known benchmark problems are considered in the experimental section, including the ZDT and the DTLZ families. To evaluate the possible differences amongst the algorithms, a carefully designed experiment is performed for the four performance metrics. The results obtained suggest that the cone-eps-MOEA is capable of presenting an efficient and balanced performance over all the performance metrics considered. These results strongly support the conclusion that the cone-eps-MOEA is a competitive approach for obtaining an efficient balance between convergence and diversity to the Pareto front, and as such represents a useful tool for the solution of multiobjective optimization problems.

The MOEADr Package - A Component-Based Framework for Multiobjective Evolutionary Algorithms Based on Decomposition

Multiobjective Evolutionary Algorithms based on Decomposition (MOEA/D) represent a widely used class of population-based metaheuristics for the solution of multicriteria optimization problems. We introduce the MOEADr package, which offers many of these variants as instantiations of a component-oriented framework. This approach contributes for easier reproducibility of existing MOEA/D variants from the literature, as well as for faster development and testing of new composite algorithms. The package offers an standardized, modular implementation of MOEA/D based on this framework, which was designed aiming at providing researchers and practitioners with a standard way to discuss and express MOEA/D variants. In this paper we introduce the design principles behind the MOEADr package, as well as its current components. Three case studies are provided to illustrate the main aspects of the package.