An embedding-based distance for temporal graphs

We define a distance between temporal graphs based on graph embeddings built using time-respecting random walks. We study both the case of matched graphs, when there exists a known relation between the nodes, and the unmatched case, when such a relation is unavailable and the graphs may be of different sizes. We illustrate the interest of our distance definition, using both real and synthetic temporal network data, by showing its ability to discriminate between graphs with different structural and temporal properties. Leveraging state-of-the-art machine learning techniques, we propose an efficient implementation of distance computation that is viable for large-scale temporal graphs.

Efficient distributed representations beyond negative sampling

This article describes an efficient method to learn distributed representations, also known as embeddings. This is accomplished minimizing an objective function similar to the one introduced in the Word2Vec algorithm and later adopted in several works. The optimization computational bottleneck is the calculation of the softmax normalization constants for which a number of operations scaling quadratically with the sample size is required. This complexity is unsuited for large datasets and negative sampling is a popular workaround, allowing one to obtain distributed representations in linear time with respect to the sample size. Negative sampling consists, however, in a change of the loss function and hence solves a different optimization problem from the one originally proposed. Our contribution is to show that the sotfmax normalization constants can be estimated in linear time, allowing us to design an efficient optimization strategy to learn distributed representations. We test our approximation on two popular applications related to word and node embeddings. The results evidence competing performance in terms of accuracy with respect to negative sampling with a remarkably lower computational time.

Nishimori meets Bethe: a spectral method for node classification in sparse weighted graphs

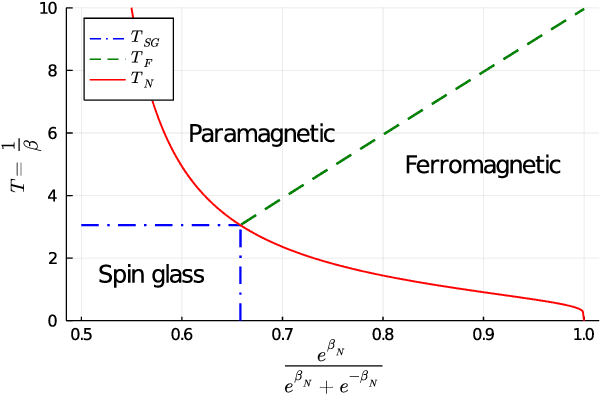
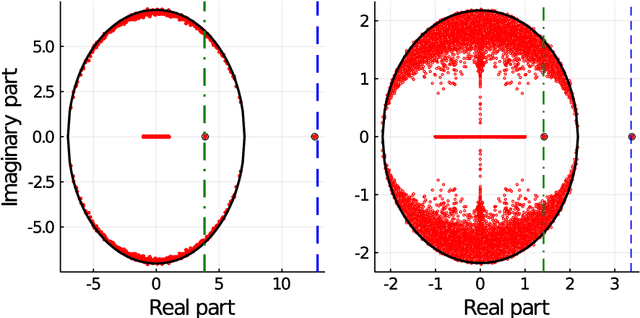
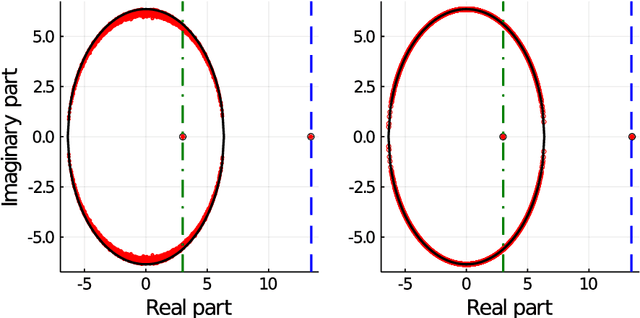
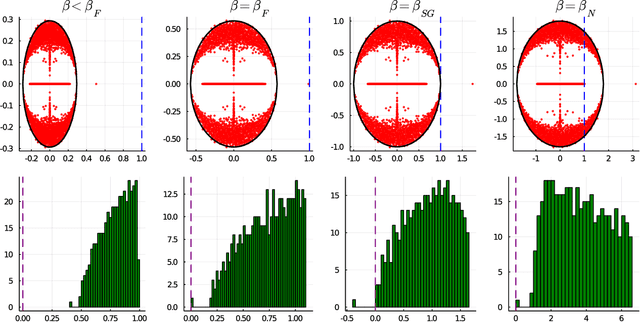
This article unveils a new relation between the Nishimori temperature parametrizing a distribution P and the Bethe free energy on random Erdos-Renyi graphs with edge weights distributed according to P. Estimating the Nishimori temperature being a task of major importance in Bayesian inference problems, as a practical corollary of this new relation, a numerical method is proposed to accurately estimate the Nishimori temperature from the eigenvalues of the Bethe Hessian matrix of the weighted graph. The algorithm, in turn, is used to propose a new spectral method for node classification in weighted (possibly sparse) graphs. The superiority of the method over competing state-of-the-art approaches is demonstrated both through theoretical arguments and real-world data experiments.

Community detection in sparse time-evolving graphs with a dynamical Bethe-Hessian

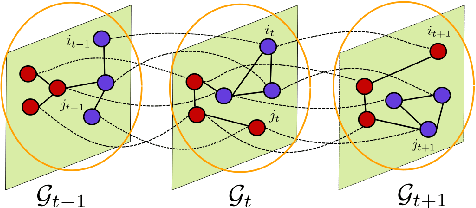
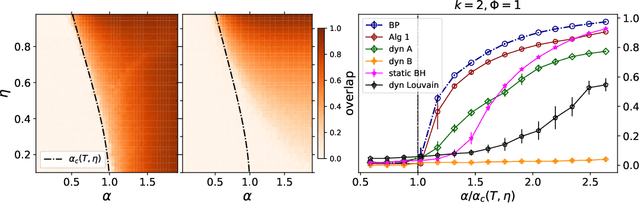
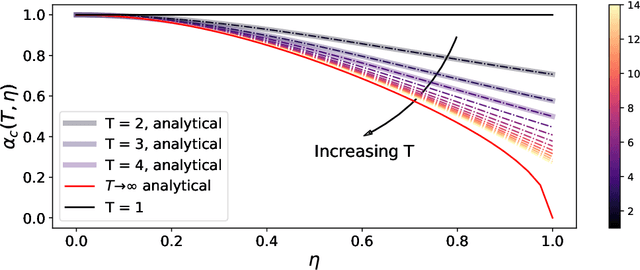
This article considers the problem of community detection in sparse dynamical graphs in which the community structure evolves over time. A fast spectral algorithm based on an extension of the Bethe-Hessian matrix is proposed, which benefits from the positive correlation in the class labels and in their temporal evolution and is designed to be applicable to any dynamical graph with a community structure. Under the dynamical degree-corrected stochastic block model, in the case of two classes of equal size, we demonstrate and support with extensive simulations that our proposed algorithm is capable of making non-trivial community reconstruction as soon as theoretically possible, thereby reaching the optimal detectability thresholdand provably outperforming competing spectral methods.

A unified framework for spectral clustering in sparse graphs

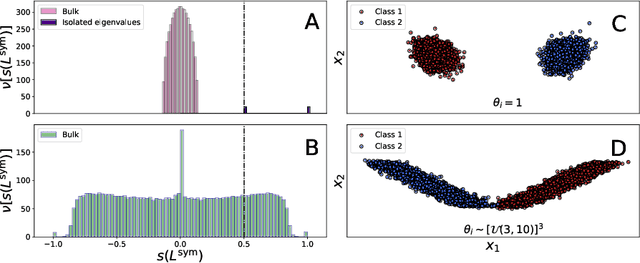
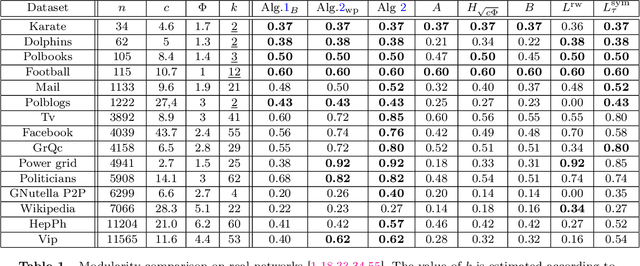
This article considers spectral community detection in the regime of sparse networks with heterogeneous degree distributions, for which we devise an algorithm to efficiently retrieve communities. Specifically, we demonstrate that a conveniently parametrized form of regularized Laplacian matrix can be used to perform spectral clustering in sparse networks, without suffering from its degree heterogeneity. Besides, we exhibit important connections between this proposed matrix and the now popular non-backtracking matrix, the Bethe-Hessian matrix, as well as the standard Laplacian matrix. Interestingly, as opposed to competitive methods, our proposed improved parametrization inherently accounts for the hardness of the classification problem. These findings are summarized under the form of an algorithm capable of both estimating the number of communities and achieving high-quality community reconstruction.

Optimal Laplacian regularization for sparse spectral community detection

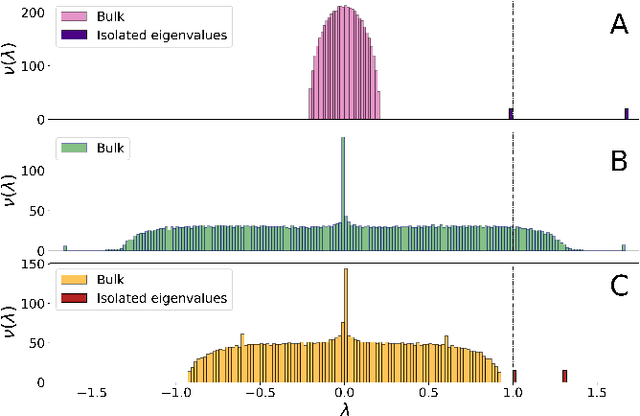
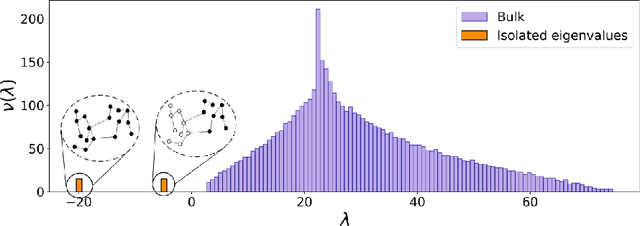
Regularization of the classical Laplacian matrices was empirically shown to improve spectral clustering in sparse networks. It was observed that small regularizations are preferable, but this point was left as a heuristic argument. In this paper we formally determine a proper regularization which is intimately related to alternative state-of-the-art spectral techniques for sparse graphs.

Optimized Deformed Laplacian for Spectrum-based Community Detection in Sparse Heterogeneous Graphs

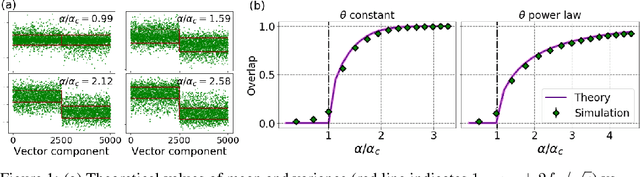
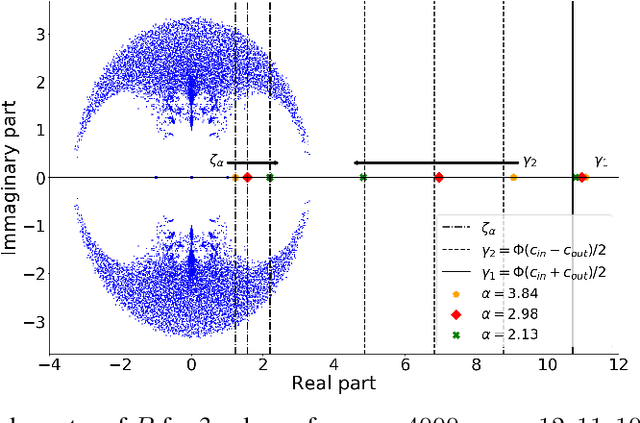
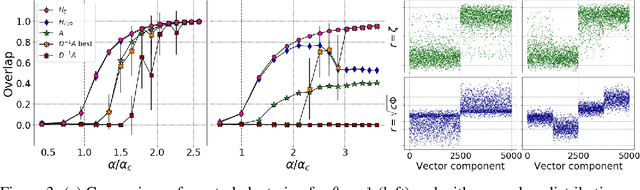
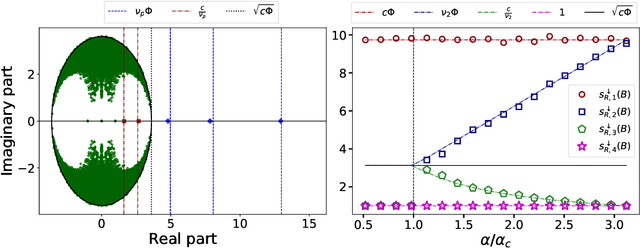
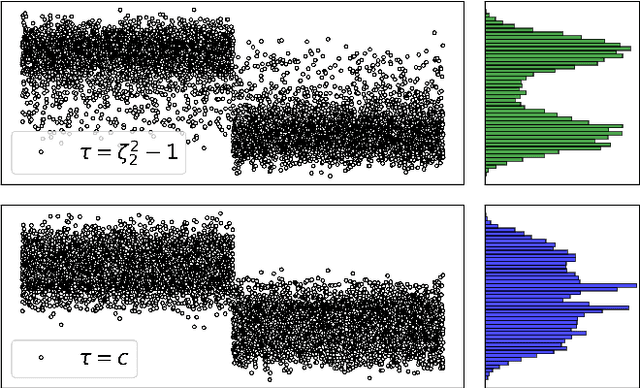
Spectral clustering is one of the most popular, yet still incompletely understood, methods for community detection on graphs. In this article we study spectral clustering based on the deformed Laplacian matrix $D-rA$, for sparse heterogeneous graphs (following a two-class degree-corrected stochastic block model). For a specific value $r = \zeta$, we show that, unlike competing methods such as the Bethe Hessian or non-backtracking operator approaches, clustering is insensitive to the graph heterogeneity. Based on heuristic arguments, we study the behavior of the informative eigenvector of $D-\zeta A$ and, as a result, we accurately predict the clustering accuracy. Via extensive simulations and application to real networks, the resulting clustering algorithm is validated and observed to systematically outperform state-of-the-art competing methods.