Optimized Deformed Laplacian for Spectrum-based Community Detection in Sparse Heterogeneous Graphs
Paper and Code
Jan 25, 2019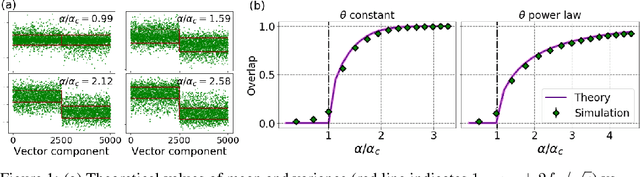

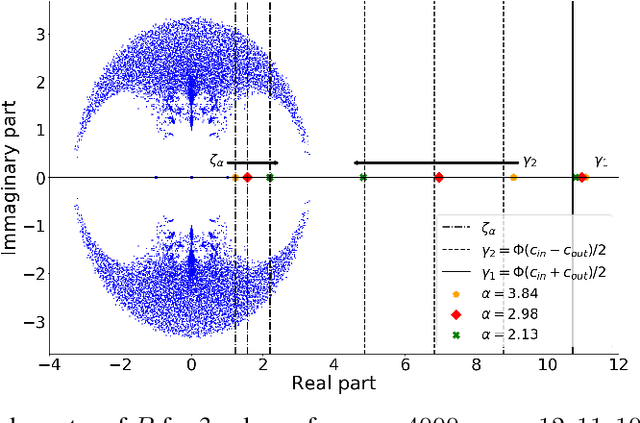
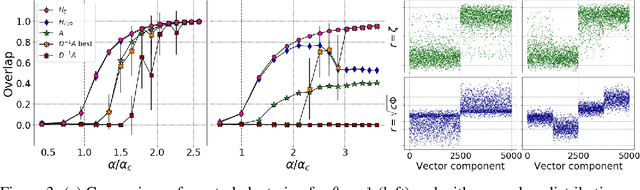
Spectral clustering is one of the most popular, yet still incompletely understood, methods for community detection on graphs. In this article we study spectral clustering based on the deformed Laplacian matrix $D-rA$, for sparse heterogeneous graphs (following a two-class degree-corrected stochastic block model). For a specific value $r = \zeta$, we show that, unlike competing methods such as the Bethe Hessian or non-backtracking operator approaches, clustering is insensitive to the graph heterogeneity. Based on heuristic arguments, we study the behavior of the informative eigenvector of $D-\zeta A$ and, as a result, we accurately predict the clustering accuracy. Via extensive simulations and application to real networks, the resulting clustering algorithm is validated and observed to systematically outperform state-of-the-art competing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge