Distributed Networked Multi-task Learning

We consider a distributed multi-task learning scheme that accounts for multiple linear model estimation tasks with heterogeneous and/or correlated data streams. We assume that nodes can be partitioned into groups corresponding to different learning tasks and communicate according to a directed network topology. Each node estimates a linear model asynchronously and is subject to local (within-group) regularization and global (across groups) regularization terms targeting noise reduction and generalization performance improvement respectively. We provide a finite-time characterization of convergence of the estimators and task relation and illustrate the scheme's general applicability in two examples: random field temperature estimation and modeling student performance from different academic districts.

Distributed Estimation via Network Regularization

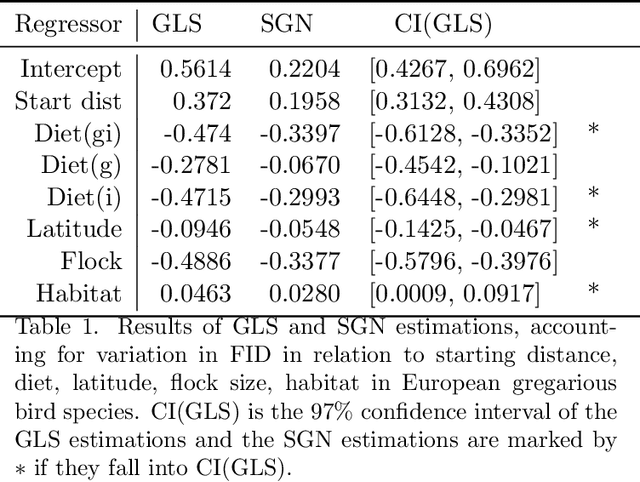
We propose a new method for distributed estimation of a linear model by a network of local learners with heterogeneously distributed datasets. Unlike other ensemble learning methods, in the proposed method, model averaging is done continuously over time in a distributed and asynchronous manner. To ensure robust estimation, a network regularization term which penalizes models with high local variability is used. We provide a finite-time characterization of convergence of the weighted ensemble average and compare this result to centralized estimation. We illustrate the general applicability of the method in two examples: estimation of a Markov random field using wireless sensor networks and modeling prey escape behavior of birds based on a real-world dataset.