Machine Learning-Guided Design of Non-Reciprocal and Asymmetric Elastic Chiral Metamaterials

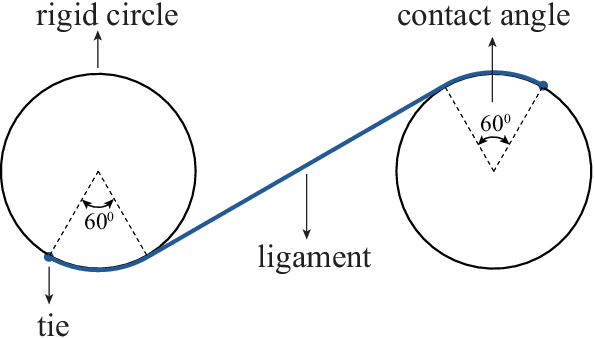
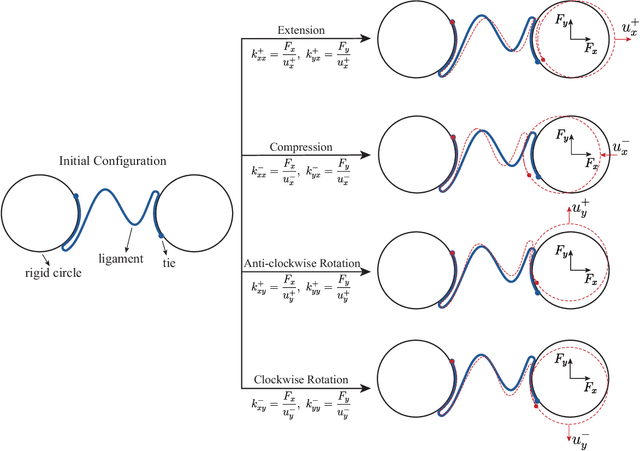
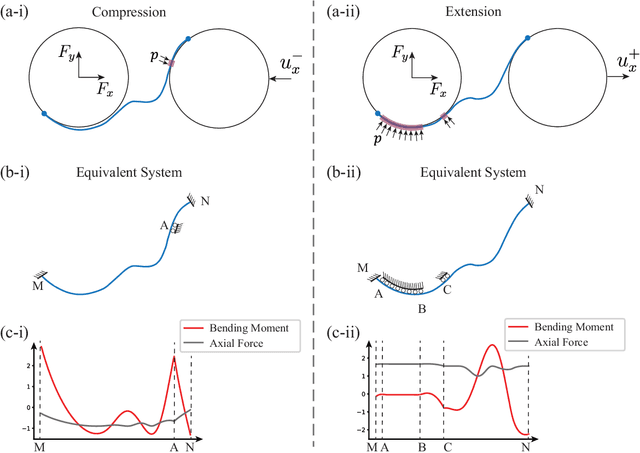
There has been significant recent interest in the mechanics community to design structures that can either violate reciprocity, or exhibit elastic asymmetry or odd elasticity. While these properties are highly desirable to enable mechanical metamaterials to exhibit novel wave propagation phenomena, it remains an open question as to how to design passive structures that exhibit both significant non-reciprocity and elastic asymmetry. In this paper, we first define several design spaces for chiral metamaterials leveraging specific design parameters, including the ligament contact angles, the ligament shape, and circle radius. Having defined the design spaces, we then leverage machine learning approaches, and specifically Bayesian optimization, to determine optimally performing designs within each design space satisfying maximal non-reciprocity or stiffness asymmetry. Finally, we perform multi-objective optimization by determining the Pareto optimum and find chiral metamaterials that simultaneously exhibit high non-reciprocity and stiffness asymmetry. Our analysis of the underlying mechanisms reveals that chiral metamaterials that can display multiple different contact states under loading in different directions are able to simultaneously exhibit both high non-reciprocity and stiffness asymmetry. Overall, this work demonstrates the effectiveness of employing ML to bring insights to a novel domain with limited prior information, and more generally will pave the way for metamaterials with unique properties and functionality in directing and guiding mechanical wave energy.

Interpreting and generalizing deep learning in physics-based problems with functional linear models

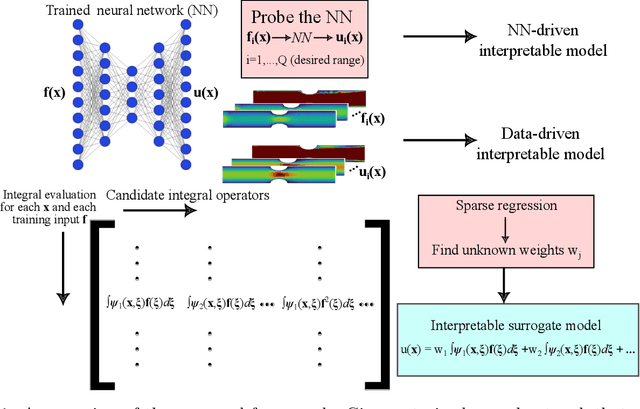
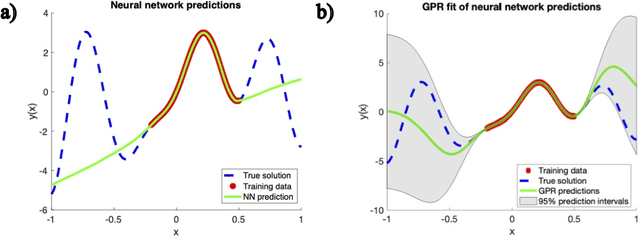
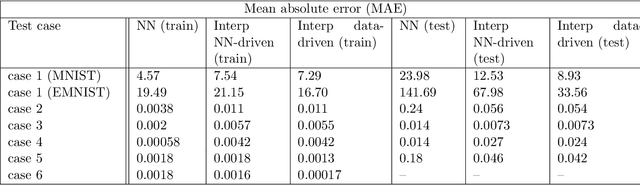
Although deep learning has achieved remarkable success in various scientific machine learning applications, its black-box nature poses concerns regarding interpretability and generalization capabilities beyond the training data. Interpretability is crucial and often desired in modeling physical systems. Moreover, acquiring extensive datasets that encompass the entire range of input features is challenging in many physics-based learning tasks, leading to increased errors when encountering out-of-distribution (OOD) data. In this work, motivated by the field of functional data analysis (FDA), we propose generalized functional linear models as an interpretable surrogate for a trained deep learning model. We demonstrate that our model could be trained either based on a trained neural network (post-hoc interpretation) or directly from training data (interpretable operator learning). A library of generalized functional linear models with different kernel functions is considered and sparse regression is used to discover an interpretable surrogate model that could be analytically presented. We present test cases in solid mechanics, fluid mechanics, and transport. Our results demonstrate that our model can achieve comparable accuracy to deep learning and can improve OOD generalization while providing more transparency and interpretability. Our study underscores the significance of interpretability in scientific machine learning and showcases the potential of functional linear models as a tool for interpreting and generalizing deep learning.

Towards out of distribution generalization for problems in mechanics

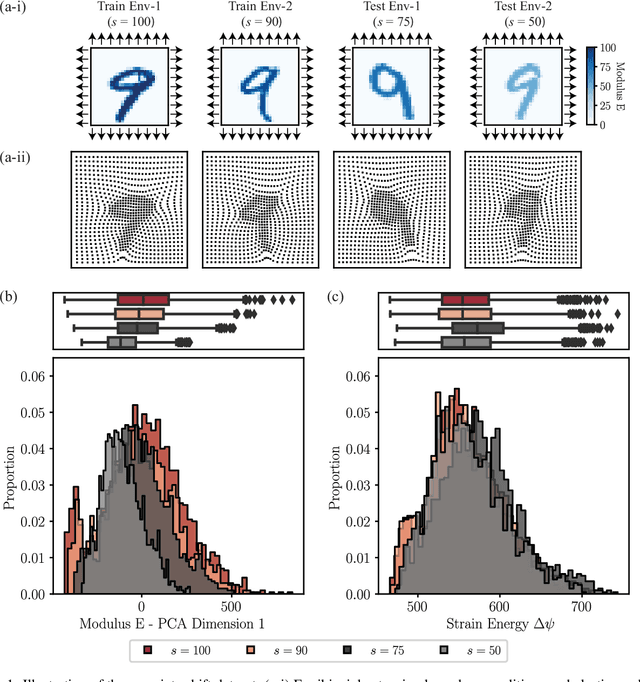
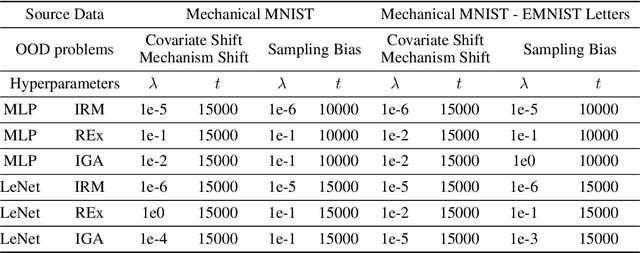
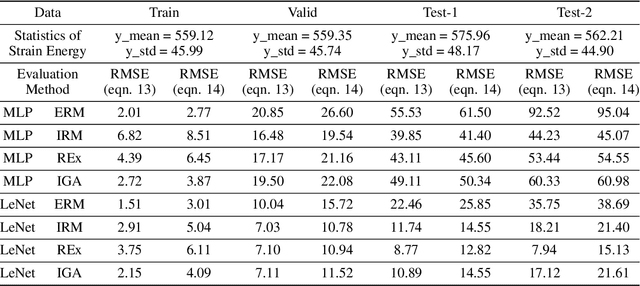
There has been a massive increase in research interest towards applying data driven methods to problems in mechanics. While traditional machine learning (ML) methods have enabled many breakthroughs, they rely on the assumption that the training (observed) data and testing (unseen) data are independent and identically distributed (i.i.d). Thus, traditional ML approaches often break down when applied to real world mechanics problems with unknown test environments and data distribution shifts. In contrast, out-of-distribution (OOD) generalization assumes that the test data may shift (i.e., violate the i.i.d. assumption). To date, multiple methods have been proposed to improve the OOD generalization of ML methods. However, because of the lack of benchmark datasets for OOD regression problems, the efficiency of these OOD methods on regression problems, which dominate the mechanics field, remains unknown. To address this, we investigate the performance of OOD generalization methods for regression problems in mechanics. Specifically, we identify three OOD problems: covariate shift, mechanism shift, and sampling bias. For each problem, we create two benchmark examples that extend the Mechanical MNIST dataset collection, and we investigate the performance of popular OOD generalization methods on these mechanics-specific regression problems. Our numerical experiments show that in most cases, while the OOD generalization algorithms perform better compared to traditional ML methods on these OOD problems, there is a compelling need to develop more robust OOD generalization methods that are effective across multiple OOD scenarios. Overall, we expect that this study, as well as the associated open access benchmark datasets, will enable further development of OOD generalization methods for mechanics specific regression problems.