Cosserat-Rod Based Dynamic Modeling of Soft Slender Robot Interacting with Environment

Soft slender robots have attracted more and more research attentions in these years due to their continuity and compliance natures. However, mechanics modeling for soft robots interacting with environment is still an academic challenge because of the non-linearity of deformation and the non-smooth property of the contacts. In this work, starting from a piece-wise local strain field assumption, we propose a nonlinear dynamic model for soft robot via Cosserat rod theory using Newtonian mechanics which handles the frictional contact with environment and transfer them into the nonlinear complementary constraint (NCP) formulation. Moreover, we smooth both the contact and friction constraints in order to convert the inequality equations of NCP to the smooth equality equations. The proposed model allows us to compute the dynamic deformation and frictional contact force under common optimization framework in real time when the soft slender robot interacts with other rigid or soft bodies. In the end, the corresponding experiments are carried out which valid our proposed dynamic model.

Piecewise Linear Strain Cosserat Model for Soft Slender Manipulator

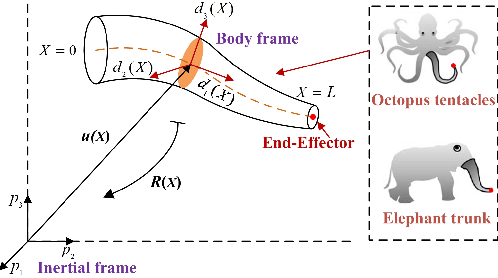
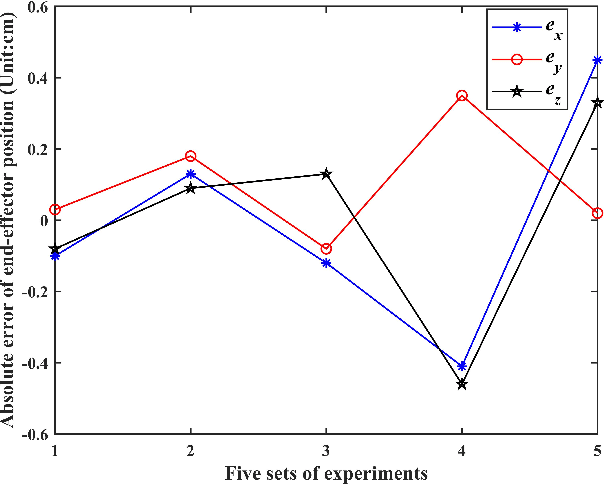
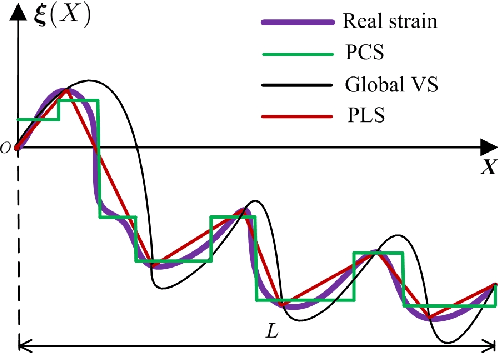
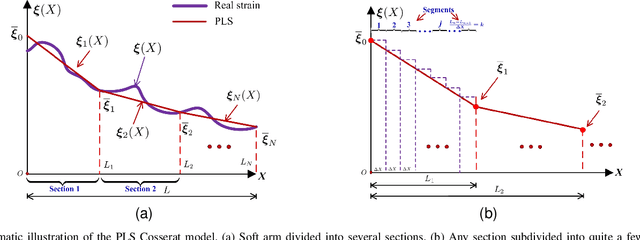
Recently soft robotics has rapidly become a novel and promising area of research with many designs and applications due to their flexible and compliant structure. However, it is more difficult to derive the nonlinear dynamic model of such soft robots. The differential kinematics and dynamics of the soft manipulator can be formulated as a set of highly nonlinear partial differential equations (PDEs) via the classic Cosserat rod theory. In this work, we propose a discrete modeling technique named piecewise linear strain (PLS) to solve the PDEs of Cosserat-based models, based on which the associated analytic models are deduced. To validate the accuracy of the proposed Cosserat model, the static model of the conical cantilever rod under gravity as a simple example is simulated by using different discretization methods. Results indicate that PLS Cosserat model is comparable to the mechanical deformation behavior of real-world soft manipulator. Finally, a parameters identification scheme for this model is established, and the simulation as well as experimental validation demonstrate that using this method can identify the model physical parameters with high accuracy.