Generating Geological Facies Models with Fidelity to Diversity and Statistics of Training Images using Improved Generative Adversarial Networks

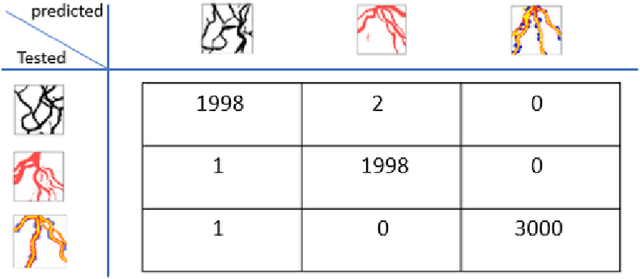
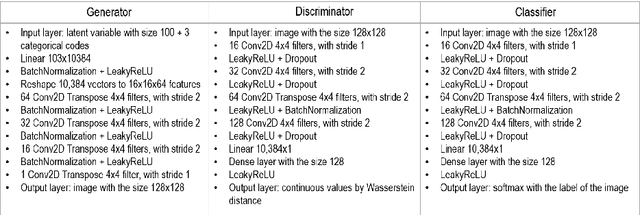
This paper presents a methodology and workflow that overcome the limitations of the conventional Generative Adversarial Networks (GANs) for geological facies modeling. It attempts to improve the training stability and guarantee the diversity of the generated geology through interpretable latent vectors. The resulting samples are ensured to have the equal probability (or an unbiased distribution) as from the training dataset. This is critical when applying GANs to generate unbiased and representative geological models that can be further used to facilitate objective uncertainty evaluation and optimal decision-making in oil field exploration and development. We proposed and implemented a new variant of GANs called Info-WGAN for the geological facies modeling that combines Information Maximizing Generative Adversarial Network (InfoGAN) with Wasserstein distance and Gradient Penalty (GP) for learning interpretable latent codes as well as generating stable and unbiased distribution from the training data. Different from the original GAN design, InfoGAN can use the training images with full, partial, or no labels to perform disentanglement of the complex sedimentary types exhibited in the training dataset to achieve the variety and diversity of the generated samples. This is accomplished by adding additional categorical variables that provide disentangled semantic representations besides the mere randomized latent vector used in the original GANs. By such means, a regularization term is used to maximize the mutual information between such latent categorical codes and the generated geological facies in the loss function. Furthermore, the resulting unbiased sampling by Info-WGAN makes the data conditioning much easier than the conventional GANs in geological modeling because of the variety and diversity as well as the equal probability of the unconditional sampling by the generator.

Sparse-promoting Full Waveform Inversion based on Online Orthonormal Dictionary Learning

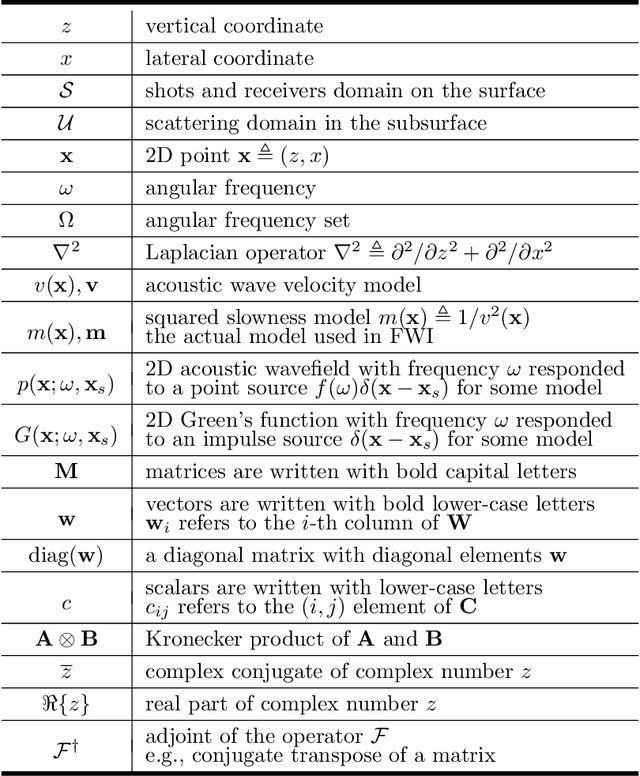
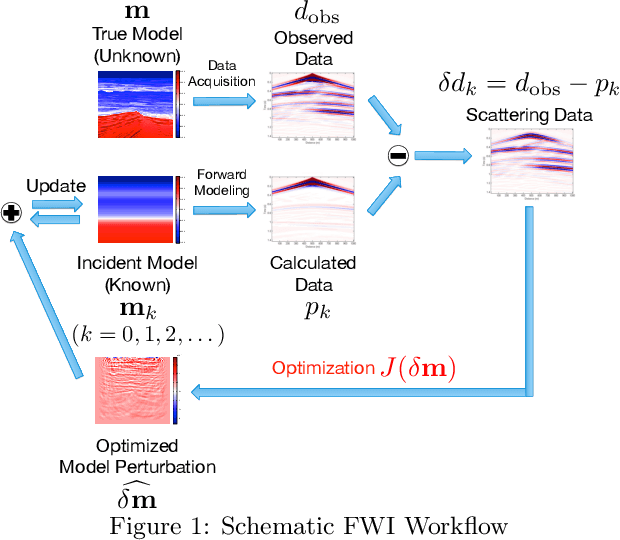
Full waveform inversion (FWI) delivers high-resolution images of the subsurface by minimizing iteratively the misfit between the recorded and calculated seismic data. It has been attacked successfully with the Gauss-Newton method and sparsity promoting regularization based on fixed multiscale transforms that permit significant subsampling of the seismic data when the model perturbation at each FWI data-fitting iteration can be represented with sparse coefficients. Rather than using analytical transforms with predefined dictionaries to achieve sparse representation, we introduce an adaptive transform called the Sparse Orthonormal Transform (SOT) whose dictionary is learned from many small training patches taken from the model perturbations in previous iterations. The patch-based dictionary is constrained to be orthonormal and trained with an online approach to provide the best sparse representation of the complex features and variations of the entire model perturbation. The complexity of the training method is proportional to the cube of the number of samples in one small patch. By incorporating both compressive subsampling and the adaptive SOT-based representation into the Gauss-Newton least-squares problem for each FWI iteration, the model perturbation can be recovered after an l1-norm sparsity constraint is applied on the SOT coefficients. Numerical experiments on synthetic models demonstrate that the SOT-based sparsity promoting regularization can provide robust FWI results with reduced computation.