A Theoretical Framework for Context-Sensitive Temporal Probability Model Construction with Application to Plan Projection

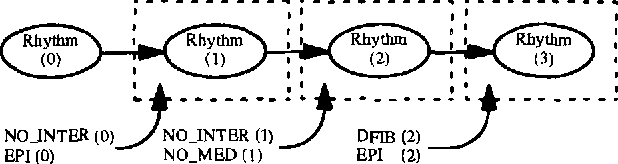
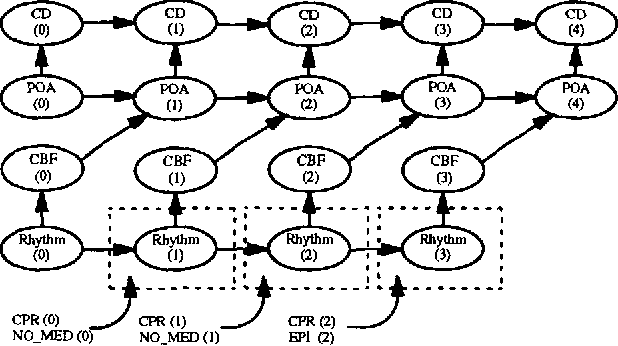
We define a context-sensitive temporal probability logic for representing classes of discrete-time temporal Bayesian networks. Context constraints allow inference to be focused on only the relevant portions of the probabilistic knowledge. We provide a declarative semantics for our language. We present a Bayesian network construction algorithm whose generated networks give sound and complete answers to queries. We use related concepts in logic programming to justify our approach. We have implemented a Bayesian network construction algorithm for a subset of the theory and demonstrate it's application to the problem of evaluating the effectiveness of treatments for acute cardiac conditions.

Probabilistic Disjunctive Logic Programming

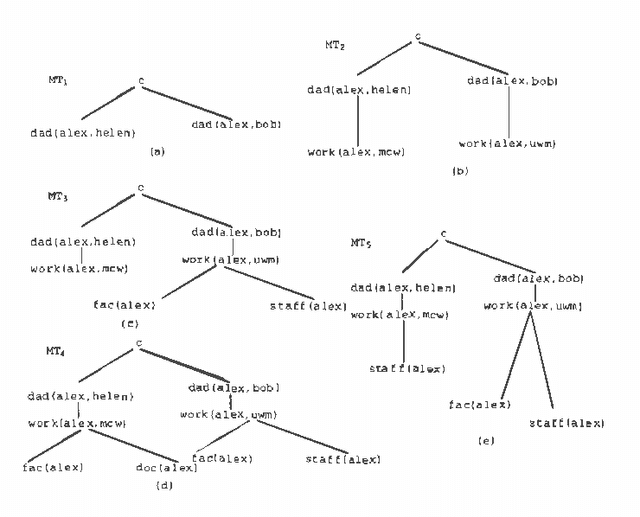
In this paper we propose a framework for combining Disjunctive Logic Programming and Poole's Probabilistic Horn Abduction. We use the concept of hypothesis to specify the probability structure. We consider the case in which probabilistic information is not available. Instead of using probability intervals, we allow for the specification of the probabilities of disjunctions. Because minimal models are used as characteristic models in disjunctive logic programming, we apply the principle of indifference on the set of minimal models to derive default probability values. We define the concepts of explanation and partial explanation of a formula, and use them to determine the default probability distribution(s) induced by a program. An algorithm for calculating the default probability of a goal is presented.