Minimum Width of Leaky-ReLU Neural Networks for Uniform Universal Approximation

The study of universal approximation properties (UAP) for neural networks (NN) has a long history. When the network width is unlimited, only a single hidden layer is sufficient for UAP. In contrast, when the depth is unlimited, the width for UAP needs to be not less than the critical width $w^*_{\min}=\max(d_x,d_y)$, where $d_x$ and $d_y$ are the dimensions of the input and output, respectively. Recently, \cite{cai2022achieve} shows that a leaky-ReLU NN with this critical width can achieve UAP for $L^p$ functions on a compact domain $K$, \emph{i.e.,} the UAP for $L^p(K,\mathbb{R}^{d_y})$. This paper examines a uniform UAP for the function class $C(K,\mathbb{R}^{d_y})$ and gives the exact minimum width of the leaky-ReLU NN as $w_{\min}=\max(d_x+1,d_y)+1_{d_y=d_x+1}$, which involves the effects of the output dimensions. To obtain this result, we propose a novel lift-flow-discretization approach that shows that the uniform UAP has a deep connection with topological theory.

Vanilla feedforward neural networks as a discretization of dynamic systems

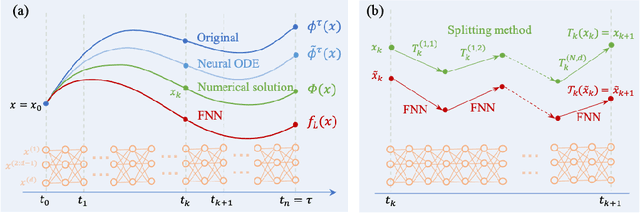
Deep learning has made significant applications in the field of data science and natural science. Some studies have linked deep neural networks to dynamic systems, but the network structure is restricted to the residual network. It is known that residual networks can be regarded as a numerical discretization of dynamic systems. In this paper, we back to the classical network structure and prove that the vanilla feedforward networks could also be a numerical discretization of dynamic systems, where the width of the network is equal to the dimension of the input and output. Our proof is based on the properties of the leaky-ReLU function and the numerical technique of splitting method to solve differential equations. Our results could provide a new perspective for understanding the approximation properties of feedforward neural networks.