A Multifactorial Optimization Paradigm for Linkage Tree Genetic Algorithm

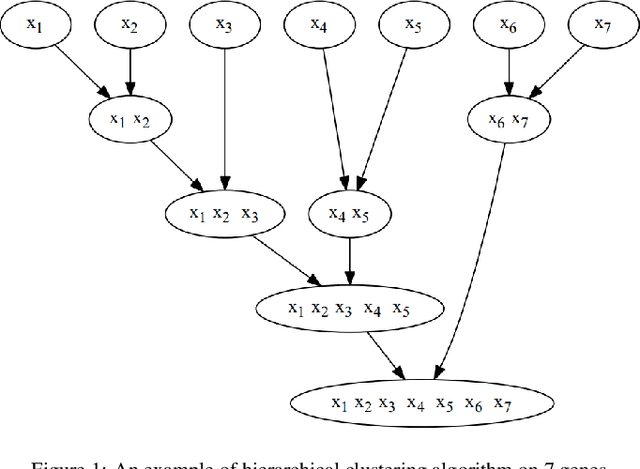
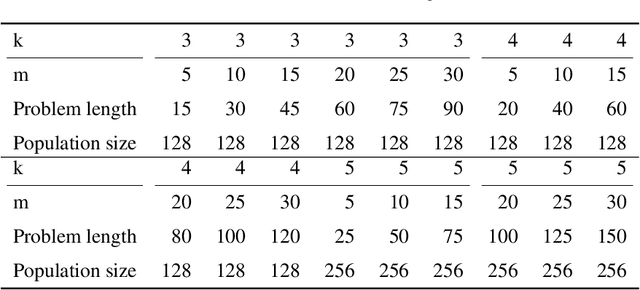
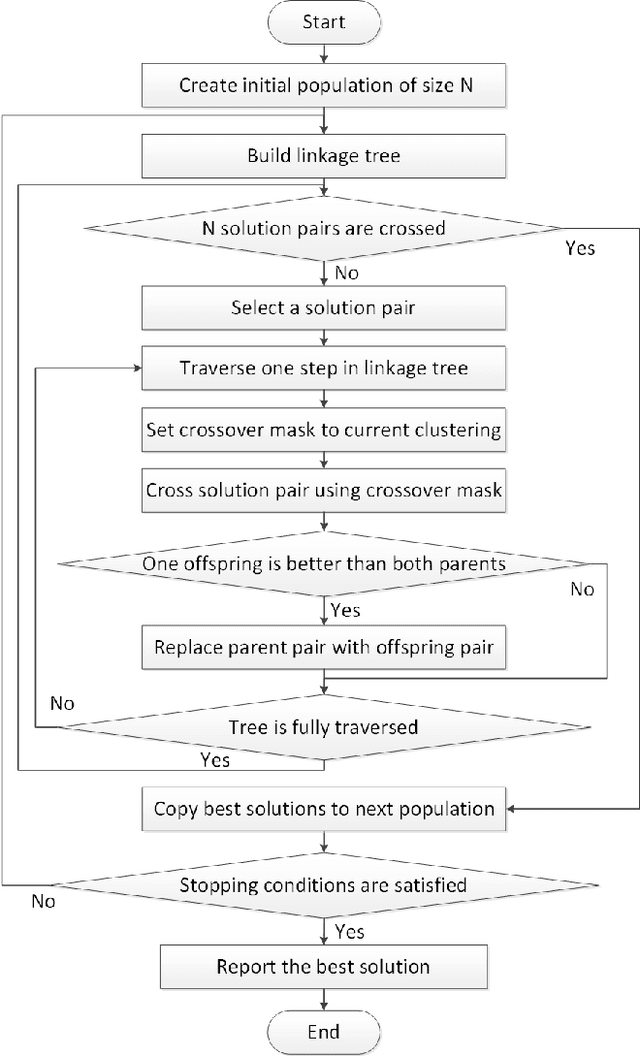
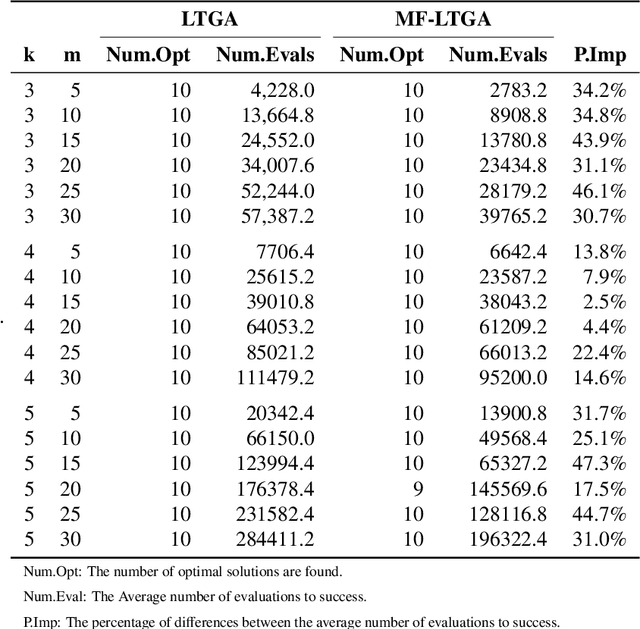
Linkage Tree Genetic Algorithm (LTGA) is an effective Evolutionary Algorithm (EA) to solve complex problems using the linkage information between problem variables. LTGA performs well in various kinds of single-task optimization and yields promising results in comparison with the canonical genetic algorithm. However, LTGA is an unsuitable method for dealing with multi-task optimization problems. On the other hand, Multifactorial Optimization (MFO) can simultaneously solve independent optimization problems, which are encoded in a unified representation to take advantage of the process of knowledge transfer. In this paper, we introduce Multifactorial Linkage Tree Genetic Algorithm (MF-LTGA) by combining the main features of both LTGA and MFO. MF-LTGA is able to tackle multiple optimization tasks at the same time, each task learns the dependency between problem variables from the shared representation. This knowledge serves to determine the high-quality partial solutions for supporting other tasks in exploring the search space. Moreover, MF-LTGA speeds up convergence because of knowledge transfer of relevant problems. We demonstrate the effectiveness of the proposed algorithm on two benchmark problems: Clustered Shortest-Path Tree Problem and Deceptive Trap Function. In comparison to LTGA and existing methods, MF-LTGA outperforms in quality of the solution or in computation time.

A Heuristic Based on Randomized Greedy Algorithms for the Clustered Shortest-Path Tree Problem

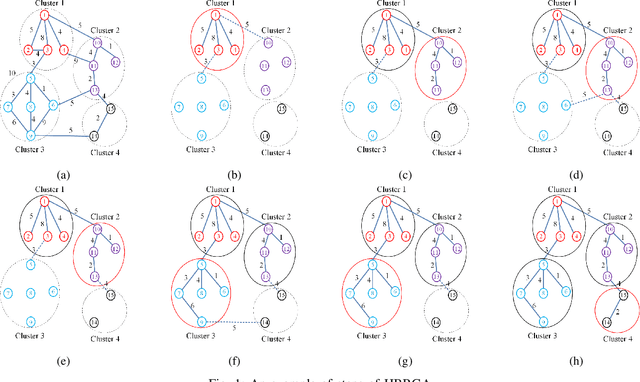
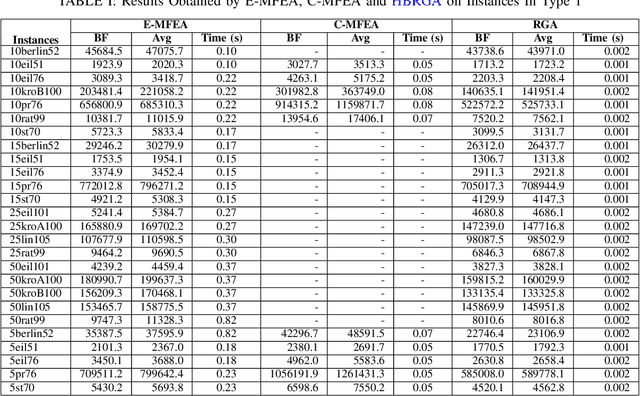
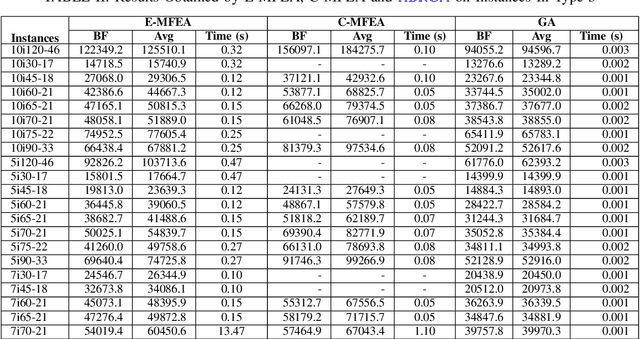
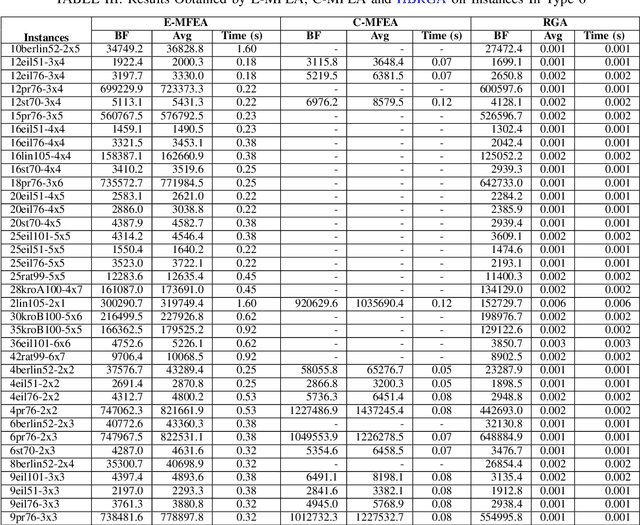
Randomized Greedy Algorithms (RGAs) are interesting approaches to solve problems whose structures are not well understood as well as problems in combinatorial optimization which incorporate the random processes and the greedy algorithms. This paper introduces a new algorithm that combines the major features of RGAs and Shortest Path Tree Algorithm (SPTA) to deal with the Clustered Shortest-Path Tree Problem (CluSPT). In our algorithm, SPTA is used to determine the shortest path tree in each cluster while the combination between characteristics of the RGAs and search strategy of SPTA is used to constructed the edges connecting clusters. To evaluate the performance of the proposed algorithm, Euclidean benchmarks are selected. The experimental investigations show the strengths of the proposed algorithm in comparison with some existing algorithms. We also analyze the influence of the parameters on the performance of the algorithm.