Tight Clusters Make Specialized Experts

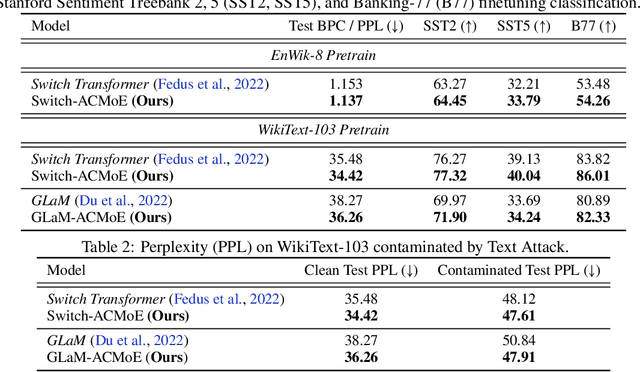
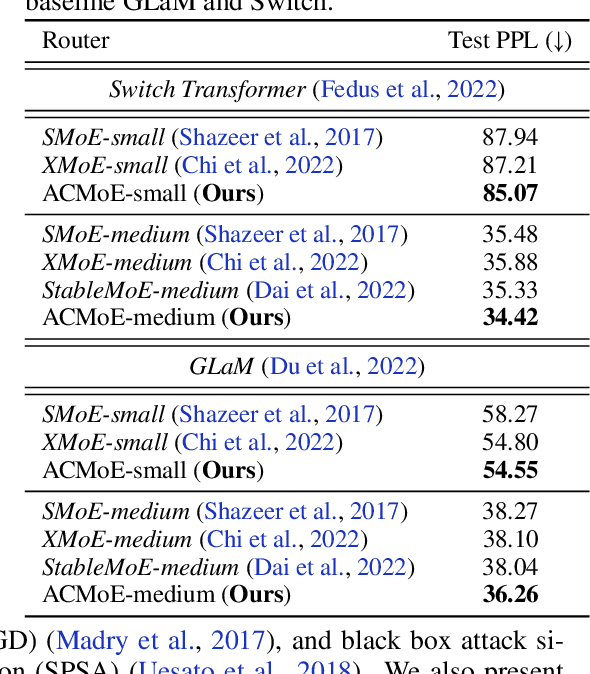
Sparse Mixture-of-Experts (MoE) architectures have emerged as a promising approach to decoupling model capacity from computational cost. At the core of the MoE model is the router, which learns the underlying clustering structure of the input distribution in order to send input tokens to appropriate experts. However, latent clusters may be unidentifiable in high dimension, which causes slow convergence, susceptibility to data contamination, and overall degraded representations as the router is unable to perform appropriate token-expert matching. We examine the router through the lens of clustering optimization and derive optimal feature weights that maximally identify the latent clusters. We use these weights to compute the token-expert routing assignments in an adaptively transformed space that promotes well-separated clusters, which helps identify the best-matched expert for each token. In particular, for each expert cluster, we compute a set of weights that scales features according to whether that expert clusters tightly along that feature. We term this novel router the Adaptive Clustering (AC) router. Our AC router enables the MoE model to obtain three connected benefits: 1) faster convergence, 2) better robustness to data corruption, and 3) overall performance improvement, as experts are specialized in semantically distinct regions of the input space. We empirically demonstrate the advantages of our AC router over baseline routing methods when applied on a variety of MoE backbones for language modeling and image recognition tasks in both clean and corrupted settings.

Elliptical Attention

Pairwise dot-product self-attention is key to the success of transformers that achieve state-of-the-art performance across a variety of applications in language and vision. This dot-product self-attention computes attention weights among the input tokens using Euclidean distance, which makes the model prone to representation collapse and vulnerable to contaminated samples. In this paper, we propose using a Mahalanobis distance metric for computing the attention weights to stretch the underlying feature space in directions of high contextual relevance. In particular, we define a hyper-ellipsoidal neighborhood around each query to increase the attention weights of the tokens lying in the contextually important directions. We term this novel class of attention Elliptical Attention. Our Elliptical Attention provides two benefits: 1) reducing representation collapse and 2) enhancing the model's robustness as the Elliptical Attention pays more attention to contextually relevant information rather than focusing on some small subset of informative features. We empirically demonstrate the advantages of Elliptical Attention over the baseline dot-product attention and state-of-the-art attention methods on various practical tasks, including object classification, image segmentation, and language modeling across different data modalities.