Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Laura M. Wolf
Continuous Herded Gibbs Sampling
Jun 11, 2021Figures and Tables:

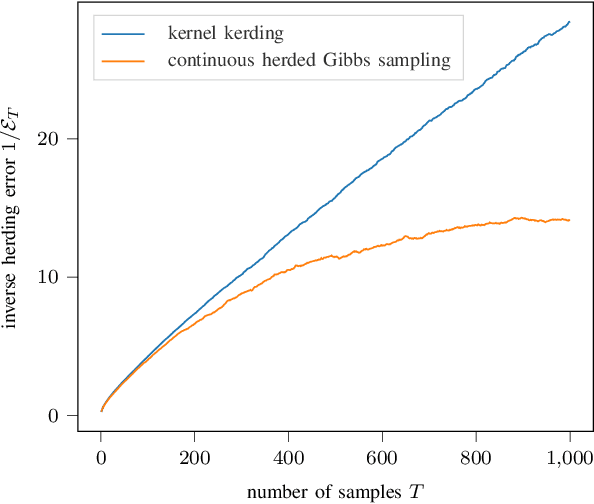





Abstract:Herding is a technique to sequentially generate deterministic samples from a probability distribution. In this work, we propose a continuous herded Gibbs sampler, that combines kernel herding on continuous densities with Gibbs sampling. Our algorithm allows for deterministically sampling from high-dimensional multivariate probability densities, without directly sampling from the joint density. Experiments with Gaussian mixture densities indicate that the L2 error decreases similarly to kernel herding, while the computation time is significantly lower, i.e., linear in the number of dimensions.
* 6 pages, 7 figures
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge